Chapter 1 | Chapter 2 | Chapter 3 | Chapter 4 | Chapter 5
Chapter 6 | Chapter 7 | Chapter 8 | Chapter 9
Appendix A | Appendix B
PREVIOUS INDEX NEXT

Chapter 7
HRC: High Resolution Camera

7.1  Status of the HRC Detectors

The HRC experienced an anomaly in its electronics on 2022-Feb-9 which necessitated a reevaluation of its operation. Both the HRC-I and the HRC-S detectors now operate using the circuitry that was being used from launch until 2020. Both instruments are operating nominally, and existing calibration products continue to be applicable. However, due to new thermal operational constraints, HRC observations are currently limited to durations of up to 14.5 ks in length. As with other spacecraft operational constraints, this maximum duration may depend upon external factors such as target pointing direction, and may be subject to further review.

7.2  Introduction and Instrument Layout

The High Resolution Camera (HRC ) is a microchannel plate (MCP) instrument comprised of two detectors, one optimized for imaging (HRC-I), and one (HRC-S) which serves as a read-out for the Low Energy Transmission Grating (LETG) discussed in Chapter 9. The HRC-I provides the largest field-of-view ( ∼  30 arcmin × 30 arcmin) of any detector aboard Chandra, and its response extends to energies below the sensitivity of ACIS (Chapter 6), albeit without comparable spectral resolution. The time resolution of the HRC detectors (16 μsec) is the best on the observatory, but can only be utilized under certain conditions as discussed in Section 7.12.
A schematic of the HRC layout is shown in Figure 7.1, and a summary of the characteristics is given in Table 7.1. A cross-section of the HRC-S layout and the relationships to the optical axis and the LETG Rowland circle are shown in Figure 7.2.
images/HRC_layout.png
Figure 7.1: A schematic of the HRC focal-plane geometry as viewed along the optical axis from the telescope towards the focal plane. See https://hea-www.harvard.edu/HRC/calib/hrccalib_a_180998.ps
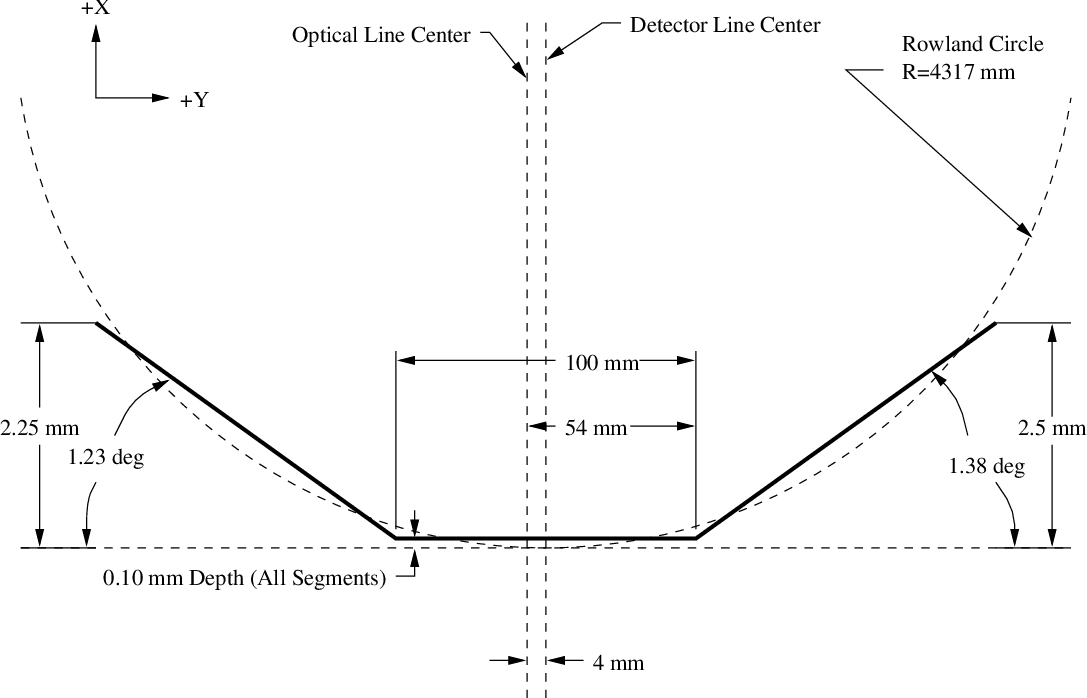
images/POG_HRC_1_3.png
Figure 7.2: A schematic cross-section of the HRC-S MCP (not to scale). The HRC-S is shifted 0.1 mm forward of the tangent plane, so the Rowland circle intersects each segment at two points.
The HRC is a direct descendant of the Einstein (Giacconi et al.  1979) and ROSAT High Resolution Imagers (HRIs) (David et al. 1996). The ROSAT HRI had the same coating (CsI) as the HRC.
The Instrument Principal Investigator is Dr. Ralph Kraft of the Smithsonian Astrophysical Observatory.
Table 7.1: HRC Parameters
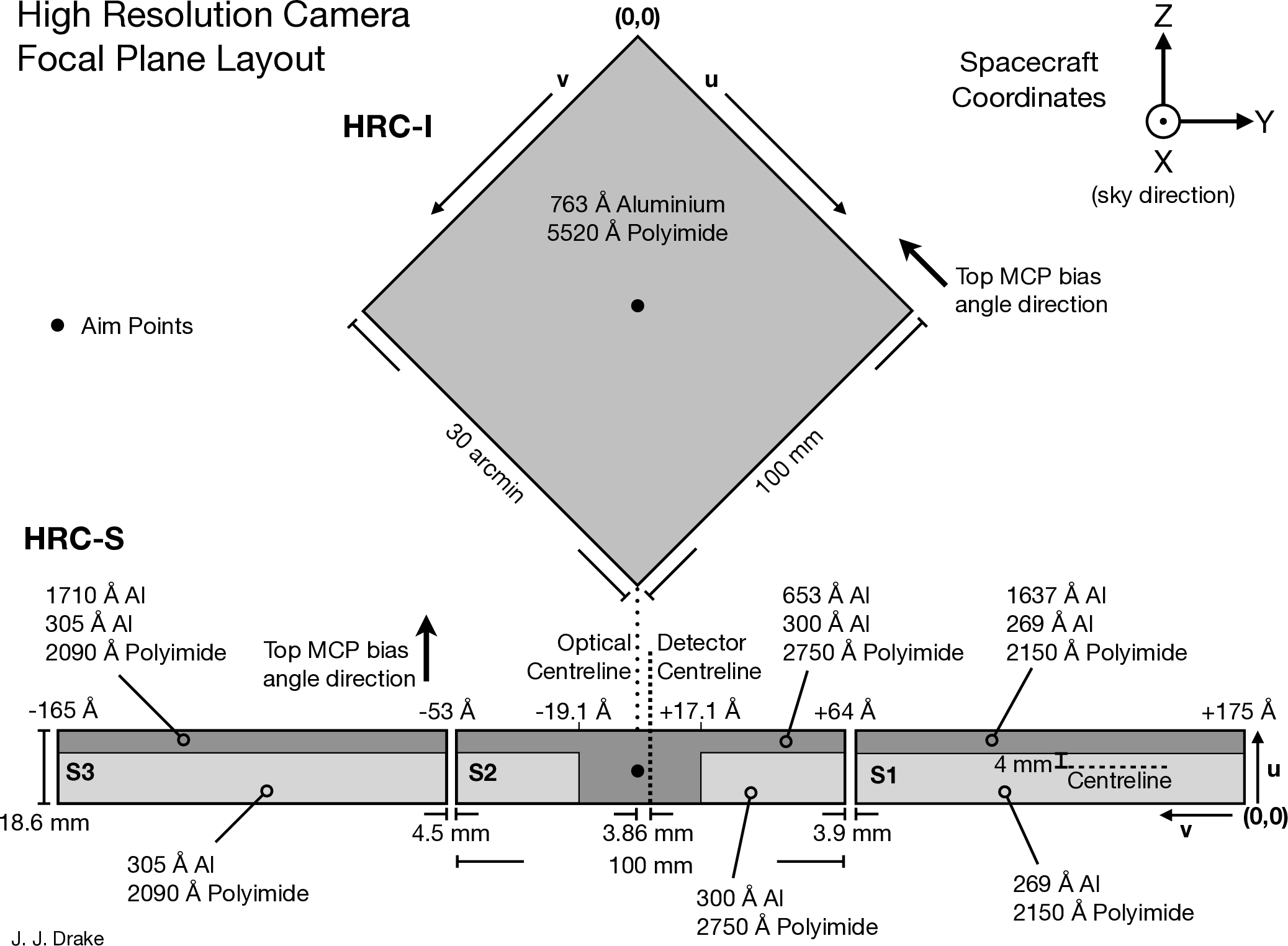
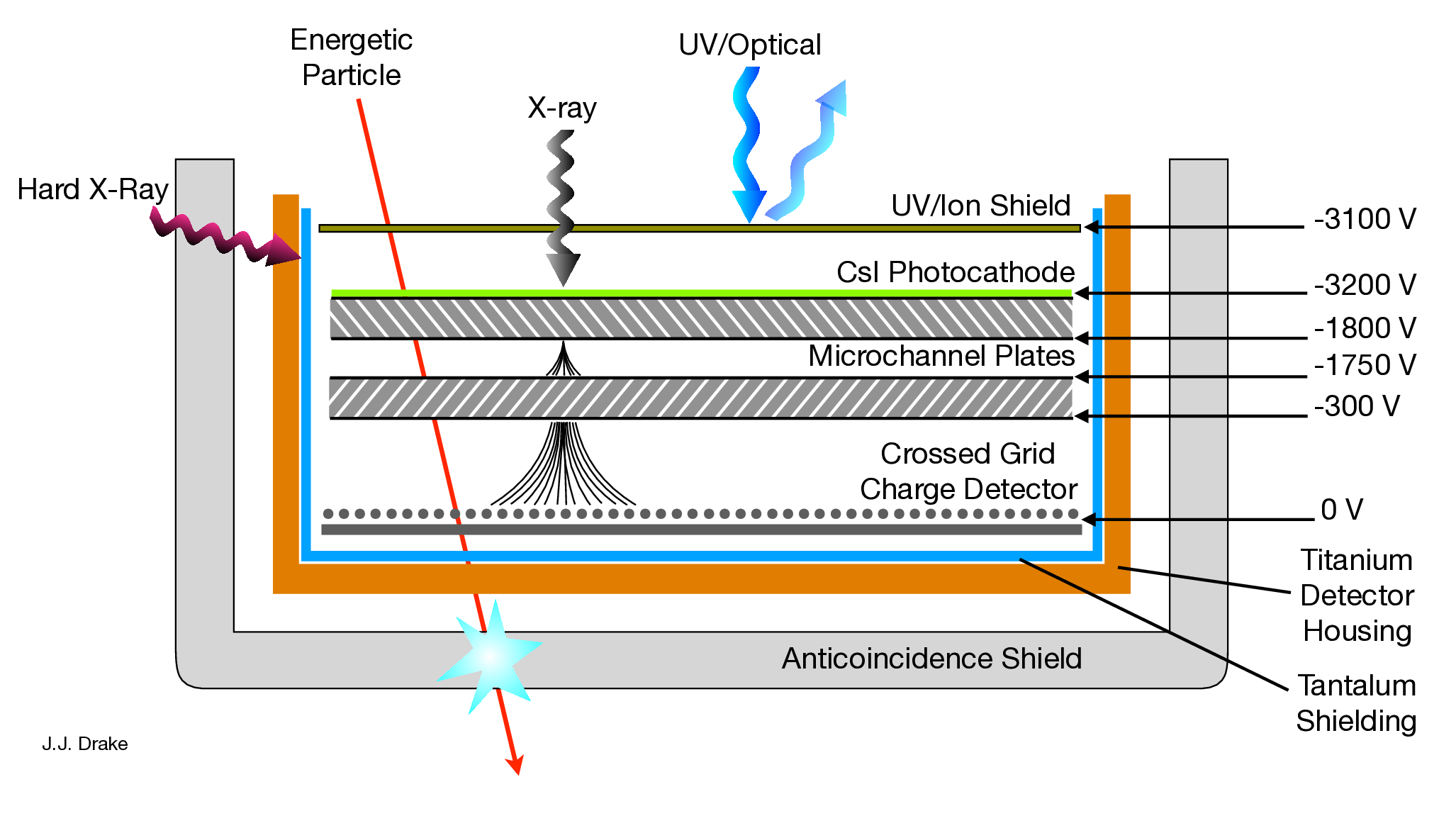
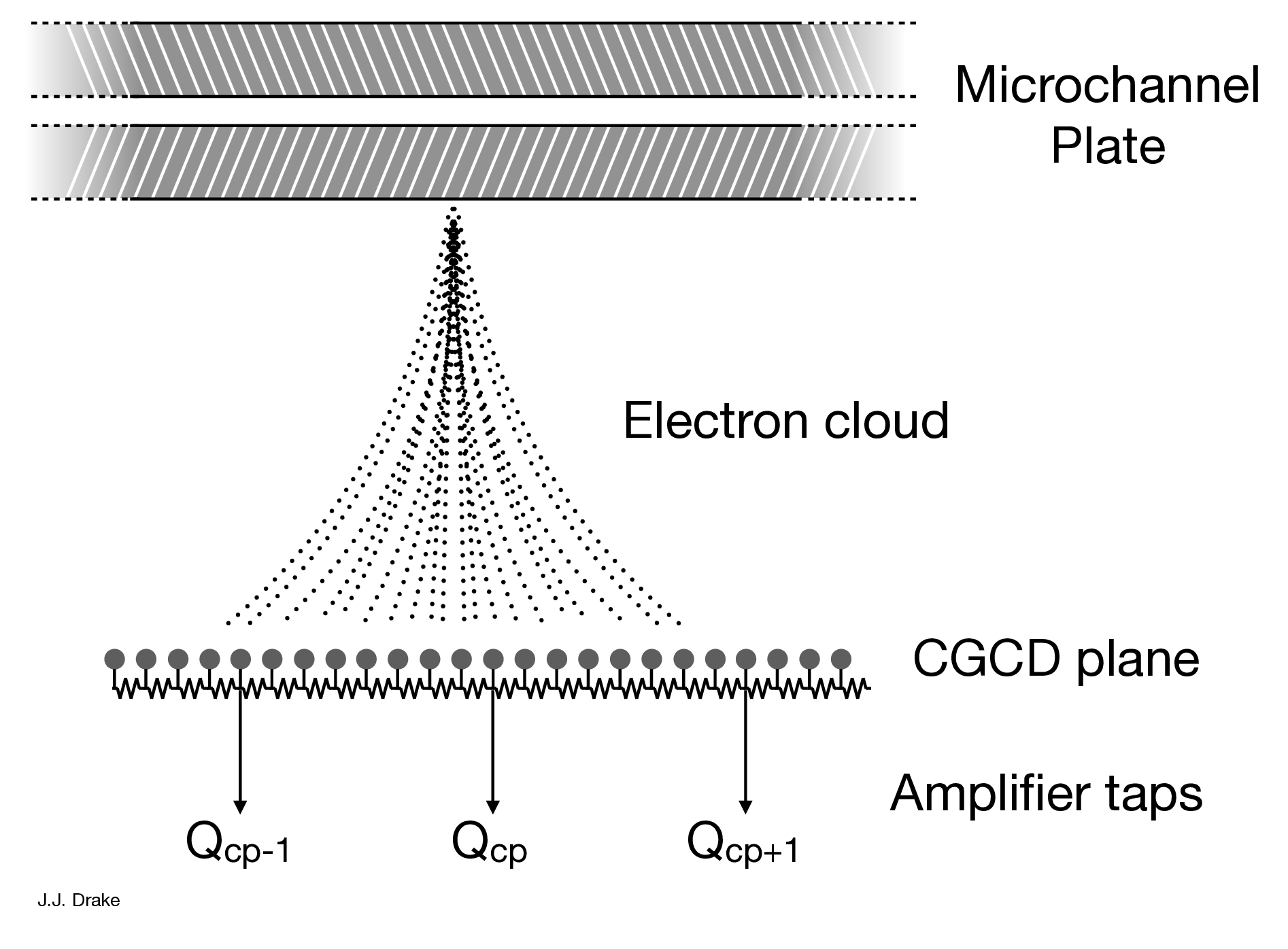
Focal-Plane Arrays
    HRC-I: CsI-coated MCP pair 90×90 mm coated
(93×93 mm open)
    HRC-S: CsI-coated MCPpairs 3-100×20 mm
Field of view HRC-I:  ∼ 30×30 arcmin
HRC-S:6×99 arcmin
MCP Bias angle:6°
UV/Ion Shields:
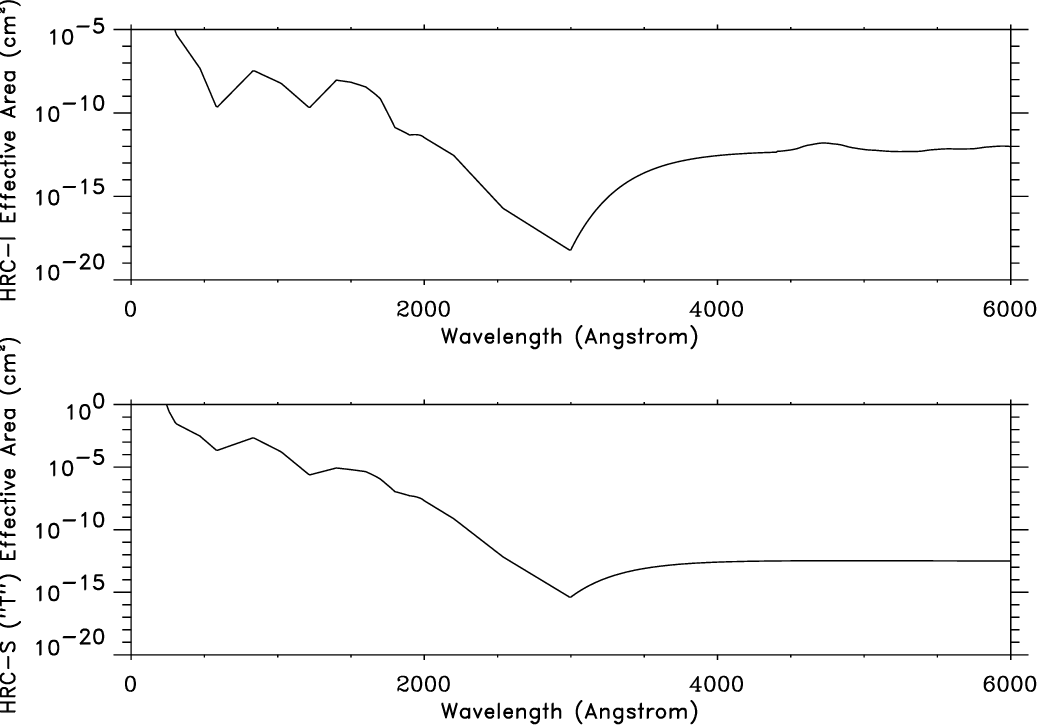
HRC-I: 5520 Å Polyimide, 763 Å Al
HRC-S:
          Inner segment (S2) 2750 Å Polyimide, 300 Å Al
          Inner segment "T" (S2) 2750 Å Polyimide, 953 Å Al
          Outer segment (S1; +1) 2150 Å  Polyimide, 269 Å Al
          Outer segment (LESF) (S1; +1) 2150 Å  Polyimide, 1906 Å Al
          Outer segment (S3; −1) 2090 Å  Polyimide, 305 Å Al
          Outer segment (LESF) (S3; −1) 2090 Å  Polyimide, 2015 Å Al
Spatial resolution FWHM  ∼ 20μm,  ∼ 0.4 arcsec
HRC-I: pore size 10μm
HRC-S: pore size 12.5μm
HRC-I: pore spacing 12.5μm
HRC-S: pore spacing 15μm
pixel size (electronic read-out)6.42938μm
[0.13175 arcsec pixel−1]
pixel size (default binning size)0.1318 arcsec pixel−1
Energy range:0.08−10.0 keV
Spectral resolution ∆E/E  ∼ 1 @1keV
MCP Quantum efficiency 30% @ 1.0 keV
10% @ 8.0 keV
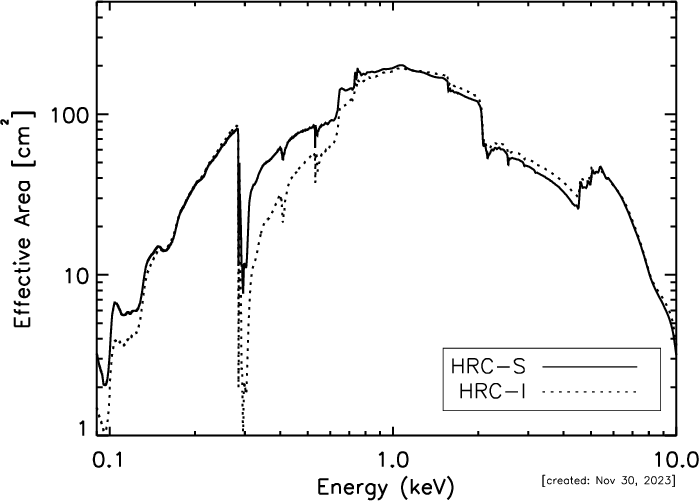
On-Axis Effective Area: HRC-I, @ .277 keV 100 cm2
HRC-I, @ 1 keV193 cm2
HRC-S, @ .277 keV 85 cm2
HRC-S, @ 1 keV 194 cm2
Time resolution 16 μsec (see Section 7.12)
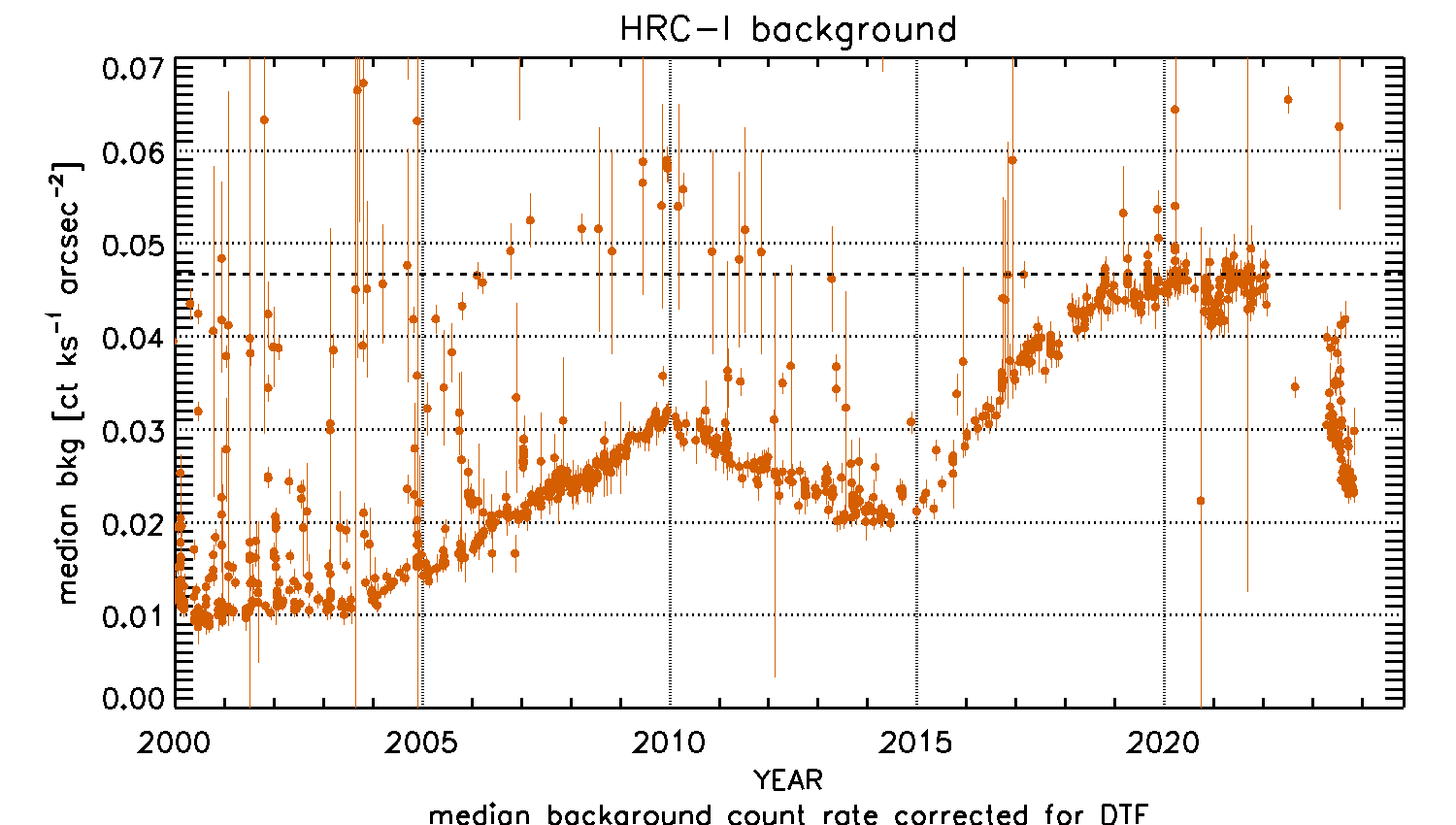
Expected QuiescentHRC-I 3.5×10−5 cts s−1 arcsec−2
background during Cycle 22 HRC-S 7.4×10−5 cts s−1 arcsec−2
in level 2 data (see Sec 7.11)
Intrinsic dead time 50 μs
Constraints: telemetry limit 184 cts s−1
maximum counts per aimpoint source 450000 cts
linearity limit (on-axis point source)
HRC-I  ∼  5 cts s−1 (2 cts s−1 pore−1)
HRC-S  ∼  25 cts s−1 (10 cts s−1  pore−1)

7.3  Basic Principles

Figure 7.3 illustrates the features of the HRC MCP s. X-rays enter through a UV/Ion shield , necessary to reduce/avoid signals from UV light, ions, and low energy electrons. Most of these X-rays are then absorbed in the CsI-coated walls of the first (input) of two consecutive MCPs. The axes of the millions of tubes that comprise the input and output MCPs are not parallel to the optical axis but are canted ("biased") at an angle of 6° in opposite directions as shown in Figure 7.3. This bias improves the probability of an interaction. The CsI coating enhances the photoemission over that from a bare MCP. The resulting photoelectrons are then accelerated by an applied electric field. The next interaction with the walls releases several secondary electrons and so on, until a cascade of electrons is produced.
images/fig7_3_jjd.png
Figure 7.3: A schematic of the HRC Microchannel-Plate detector.
One purpose of the second (output) MCP is to provide additional gain. In addition, reversing the direction of the second MCP's bias angle with respect to the first removes a clear path for positive ions, and hence reduces the possibility of (positive) ion feedback - where an accelerated ion moving in the opposite direction as that of the electrons ends up causing the release of electrons and starts the process all over again.
The electron cloud - typically about 2×107 electrons per photon - that emerges from the output MCP is accelerated towards a position-sensitive charge detector. The HRC employs two types of charge detectors: the HRC-I uses a crossed grid charge detector , while the HRC-S uses a hybrid where one axis is comprised of wires and the other has gold lines deposited on a ceramic substrate. Adjacent wires (or lines) are resistively connected and every eighth wire is attached to a charge-sensitive amplifier, referred to as a "tap", as illustrated in Figure 7.4.
The X-ray position is determined by calculating the centroid of the charge cloud exiting the rear MCP via the "three tap algorithm". In short, the three tap algorithm determines the charge cloud centroid using a combination of digital and analog electronics and off-line processing. Fast discriminators and logic circuits first determine a "coarse" position, which is based on the amplifier with maximum detected charge. Analog switches then select the three amplifiers centered on that coarse position and steer them to analog-to-digital converters. The coarse position and three digitized values are then telemetered to the ground and used off-line to calculate the event position. This process is performed for each axis. The reconstructed X-ray position can then be written as the sum of a coarse position and a charge centroid term centered on the coarse position:
pos = cpi + ( Qcpi+1 − Qcpi−1
Qcpi−1 + Qcpi + Qcpi+1
 )×∆
(7.1)
where cp is the coarse position, Qcpi+1 is the charge measured on the cpi+1 tap, and ∆ is the distance between taps. Since the charge cloud extends beyond the two outer taps, each of the outer amplifiers underestimates the amount of charge needed to calculate the true centroid. For an event perfectly centered on the middle tap, the amount of charge missed by the two outer taps cancel in the equation. If however, the event position is not over the center of a tap, the fractional amount of missing charge is different and produces a small systematic error in the reconstructed position. The small systematic positional error combined with the coarse position logic produce "gaps" in the HRC images. These gaps are perfectly aligned with the detector axes and correspond to positions exactly half-way between amplifier taps. The gaps are systematic and are removed in data processing.
images/fig7_4_jjd.png
Figure 7.4: Schematic representation of event position determination for one axis of the crossed grid charge detector (CGCD). The electron cloud is divided between several amplifiers. The position of the event relative to the central coarse position, fp, is calculated from the difference between the signals on either side of th e coarse position p (Qcp−1, Qcp+1), divided by the sum of the three signals, fp = [(Qcp−1 − Qcp+1)/(Qcp−1 + Qcp + Qcp+1)].
The three-tap position algorithm described above can be improved upon by making use of the predictability of the shape of the charge cloud exiting the rear MCP. The spatial distribution of the charge cloud leaving the rear of the second MCP has a very specific shape for X-ray induced events. This shape has often been modeled as the combination of a Gaussian and a Lorentzian distribution. Due to this specific shape, it has been observed and simulated via Monte Carlo techniques that the fine position term:
( Qcpi+1 − Qcpi−1
Qcpi−1 + Qcpi + Qcpi+1
 )
(7.2)
and the complementary term:
( Qcpi
Qcpi−1 + Qcpi + Qcpi+1
 )
(7.3)
are highly correlated. In fact, a scatter plot of these two quantities for X-ray induced events closely describes a hyperbola. Non X-ray events, primarily those due to the passage of charged particles, produce charge distributions that are often larger and more spatially extended and complex. As such, it is possible to remove many non-X-ray background events by filtering out those events that do not fit the hyperbola. Furthermore, since the charge distribution is centrally peaked, the complement Qcpi term is larger and less susceptible to noise-induced errors than the Qcpi+1 −Qcpi−1 difference term. It is therefore possible to use the complement term, and the best fit hyperbolic locus, to correct those events where instrumental noise has compromised the three-tap fine position. A much more detailed explanation of this technique is presented in Murray, et al. (2000).
For more details concerning the HRC see Murray & Chappell (1989) and Zombeck et al. (1995).

7.3.1  Aimpoints

The aimpoints are the positions on the instrument where the flux from a point source with no commanded offsets is placed. Note that unlike ACIS, where the aimpoint position is offset by ≈ 10−20 arcsec from the optical axis1, there are no offsets for the HRC. Offsets may be set for spectroscopic observations on the HRC-S (see Section 9.3.1). There are two nominal aimpoints (see Table 4.3) as indicated in Figure 7.1 - one at the approximate center of the HRC-I, and the other slightly off-center on HRC-S. The HRC-S aimpoint Z-offset places the LETG-dispersed image along the centerline of the thinner part of the UV/Ion Shield (the two white rectangles in the diagram; see Section 7.9). The HRC-S aimpoint Y-offset is slightly off-center, so that the boundaries between the three HRC-S segments correspond to different wavelengths of the grating-dispersed spectrum (see Chapter 9 for details).

7.3.2  Drift Correction

The Chandra aimpoint is known to drift relative to the optical axis by 10-25 arcsec (Sec 5.4.3; see also Sec 4.5). This drift has been attributed to temperature fluctuations in the Aspect Camera Assembly. As a result, the nominal aimpoint is offset from the optical axis by the amount of the drift. This offset has no effect on the accuracy of the astrometry. Nominal aimpoints are expressed in terms of a permanent default aimpoint with an associated error box, as explained in 4.5. An automatic offset correction is applied to all ACIS observations to position the nominal pointing near the permanent default aimpoint (see 6.11). However, such corrections are not applied to HRC observations, since the HRC does not have instrumental structures like node boundaries or chip gaps that require careful positioning of the source on the detector. Displacement of HRC pointings due to uncorrected aimpoint drift is comparable to the magnitude of aspect dither, and has a negligible effect on the measured rate and the shape of the PSF.

7.4  Shutters

Attached to the HRC are two mechanical blades that serve as shutters. These shutters were used to block out portions of the incident flux to aid in focusing the HRC. The blade position settings are variable and were designed to allow one to block the zero-order image of a grating observation. Currently only one blade is functional, and we do not offer use of this shutter as an observing option.

7.5  Dither

The spacecraft is dithered during all observations in a Lissajous figure. For observations with the HRC, the dither amplitude is 40 arcsec peak-to-peak, with nominal periods of 1087 (in Y) and 768 (in Z) sec. Dithering serves to average out pixel-to-pixel variations in the detector response. It also ameliorates gaps in spectral coverage with the LETG/HRC-S combination caused by the HRC-S intersegment spaces near -50 Å and +60 Å (see Figure 7.1). Large amplitude dither has also been used to carry out low-resolution differential filter photometry across the thick/thin filter boundary on the HRC-S (Drake et al. 2020). Observers who need to use non-nominal dither amplitudes should consult with the instrument team. The effects of dither are corrected for during ground processing.

7.6  Spatial Resolution & Encircled Energy

Imaging with the HRC is best performed with the HRC-I because of the much lower background (Section 7.11) and larger field of view. The intrinsic PSF of the HRC is well modeled by a Gaussian with a FWHM of  ∼ 20 μm ( ∼  0.4 arcsec). The HRC pixels, determined by the electronic read-out (not the pore size), are 6.42938 μm (0.13175 arcsec). The HRC response is thus well matched to the intrinsic HRMA resolution (Chapter 4).
Approximately 90% of the encircled energy lies within a 14 pixel diameter region (1.8 arcsec) from the center pixel for the observation of AR Lac shown in Figure 7.5. The measured PSF is as good or better than the simulations because a very conservative pre-flight estimate of the aspect solution was used in the simulations.
Deconvolution of aimpoint AR Lac and Capella observations carried out at different parts of the detector show that an anomalous feature developed c.2003 (Juda & Karovska 2010). While initially suspected to be due to detector blur, it has since been verified to be present in ACIS data as well (Kashyap 2010). The Chandra PSF shows an unexplained enhancement in the profile at distances of ≈ 0.8 arcsec from the source centroid (see §4.2.3). This anomaly is in excess of that expected from ray trace simulations, and is preferentially oriented towards the mirror spherical coordinate angle of φ = 285° (see the CIAO caveats page https://cxc.harvard.edu/ciao/caveats/psf_artifact.html), and is approximately oriented towards the spacecraft +Z axis (see Figure 1.2). The asymmetry is illustrated for an HRC-I observation of an on-axis pointing of AR Lac in Figure 4.18, and the magnitude of the asymmetry is illustrated for a number of low-count-rate on-axis point sources in Figure 4.20. Figure 7.6 depicts the anomaly for Capella observations carried out at different parts of the detector. The HRC read-out blurs event locations, and contributes an additional broadening of the HRMA PSF. Based on an analysis of transient hotspots, the intrinsic detector blur has been modeled as a combination of a Gaussian and an offset Beta profile, and is incorporated in the ray trace model.
We have constructed an empirical PSF by combining on-axis HRC-I observations of AR Lac (Kashyap & Jerius 2016, https://cxc.harvard.edu/cal/Hrc/PSF/empPSF.html). This PSF minimizes blurring caused by detector effects by excluding events that are affected by tailgating (see §7.12), removing distortions induced by degapping offsets between adjacent taps, and using only the lower gain events that have more reliable determinations of event positions.
images/hrma_ee_aspect_hrc_i_point_obs_guide.png
Figure 7.5: The predicted and observed fractional encircled energy as a function of radius for an on-axis source observed with the HRMA/HRC-I. The solid black curve shows the empirical PSF, based on accumulated AR Lac observations, representing the current best sharpness achievable. Raytrace models at different energies (dashed red for 0.28 keV, dash-dotted green for 1.5 keV, and dotted blue for ≈ 6.4 keV) are also shown for qualitative comparison. The raytraces incorporate HRC-I detector blur and aspect dither for a set of representative on-axis AR Lac observations but do not include other effects.
The imaging resolution of the HRC-I degrades off-axis for two reasons: the HRMA PSF increases in size with increasing off-axis angle, and the deviation increases between the flat HRC-I detection surface and the curved HRMA focal surface. The off-axis imaging behavior of the HRC-I is shown in Figure 7.7. The nominal best-focus of the HRC-I is chosen to provide the best image quality in the center of the field-of-view.
images/hrma_anomaly_hrci_capella.png
Figure 7.6: The PSF anomaly illustrated with HRC-I observations of Capella over different locations on the detector. Two observations close to the nominal aimpoint (ObsIDs 6559, 8360; top row) are shown along with two at the extreme ends of the detector (ObsIDs 6558, 8343; bottom row). Each panel is also labeled with the detector (U,V) coordinates that the sources span. The observations have slightly different roll angles, and the direction of the anomaly is indicated with an arrow of length 0.8 arcsec. An asymmetry is discernible within each of the annuli (centered on the sources and spanning 0.8 arcsec - 1.2 arcsec); there is an excess of counts in the direction of the anomaly. (ObsID 6558 also shows an asymmetry pointing towards the bottom right, towards the detector −U direction, which is due to residual ghost events (§7.11).
images/hrma_ee_offaxis_hrci.png
Figure 7.7: Encircled energy as a function of source off-axis angle for 50% and 90% encircled energy for 1.49 and 6.40 keV for the combined HRMA/HRC-I. A conservative contribution from the aspect solution is included (FWHM = 20 μm (0.41 arcsec)). A plot for the HRC-S would be almost identical since the PSFs of the two instruments are virtually identical.

7.7  Energy Resolution

7.7.1  Non-Dispersive Energy Resolution

The intrinsic energy resolution of the HRC is poor. Even though the pulse-height amplitude (PHA) of each event is telemetered, spectral fitting cannot be usefully carried out for sources observed with the HRC. For low-resolution spectra such as these, standard spectral analysis techniques or visualization strategies cannot be used. In particular, analysis must only be done in channel space, and plots made in energy or wavelength space will convey no useful information.

7.7.2  Dispersive Energy Resolution

The HRC-S is optimized for use with the Low Energy Transmission Grating to become the Low Energy Transmission Grating Spectrometer (LETGS; see §9). The HRC-I can also be used but, because the HRC-I surface is flat and does not follow the Rowland circle, sharp spectral features cannot be measured as well as on the HRC-S. Furthermore, the wavelength coverage of the HRC-I is smaller than that of the HRC-S because of its smaller lateral extent.
The High Energy Transmission Grating (HETG) is unsupported in CIAO for use with HRC at this time. Nevertheless, observations have been carried out in the HETG+HRC-I configuration (see §8).

7.8  Gain Variations

There are significant spatial and temporal gain variations present in both instruments (see Figures 7.8, 7.9). Gain correction maps, available since CALDB v3.2.5, correct the spatial variations (for both HRC-I and HRC-S) as well as correct for the temporal gain drop (for the HRC-I). These multiplicative gain correction files transform the measured PHA values to Pulse Invariant (PI) values that are uniform across the detector (to ≈ 5% over a tap) and correspond to the PHA values seen early in the mission. Note that starting from CIAO v4.2/CALDB v4.2, the gain map is applied to the scaled sum of the amplifier signals (SUMAMPS) rather than to PHA to generate a better behaved PI distribution (Wargelin 2008, Posson-Brown & Kashyap 2009). Because of the decline in gain, more events fall below the lower level discriminator (typically set at PHA=8, set at PHA=21 in the HRC-S timing mode) in recent years, leading to a loss of effective area of as much as 10-15%. Because of this, simple multiplicative corrections to the PHA or SUMAMPS distribution do not restore the shape of the distribution to what it was early in the mission. A more accurate correction may be computed by matching the observed SUMAMPS > 50 distribution to a template distribution for a source with a soft or hard spectrum-like HZ 43 or AR Lac-using a linear transformation of SUMAMPS (i.e., corrected SUMAMPS = gC + gS ·SUMAMPS) and then obtaining a temporal polynomial fit to describe gC and gS as functions of time (see, e.g., McEntee et al. 2022). For instance, transforming the profiles of AR Lac in HRC-I to match that of ObsID 1385 results in
gC
=
1.85 + 6.97 ·Y − 0.71 ·Y2 + 0.022 ·Y3
gS
=
1.00 + 0.05 ·Y − 6.04 ×10−3 ·Y2 + 3.91 ×10−4 ·Y3  ,
(7.4)
where Y=(Decimal Year−2000), for the times prior to the HRC-I voltage increase, Y < 21.12. In order to restore the PHA and SUMAMPS distributions to what they were earlier, and thus partially mitigate the QE loss that was occurring due to gain decline, the voltage on the HRC detectors has been increased. That on the HRC-S was increased twice, first in 2012-March and again in 2021-May; the voltage on the HRC-I was increased in 2021-March. See also Chapter 9 for details. Since the power supply anomaly (see Section 7.12), the gain drop has continued and the corresponding QE loss is ≈ 10%. We therefore recommend carrying out gain profile corrections using methods as described in Equation 7.4 above.
images/fig_7_8_hrcigain.png
Figure 7.8: Gain decline on the HRC-I. The distribution of the scaled sum of the amplifier signals (scaled SUMAMPS) at each year, obtained from AR Lac observations at the aimpoint, is shown as vertical shaded stripes using square-root scaling. Higher values are shown as darker. Note the steady decline in the mode of the scaled SUMAMPS distribution with time; the distribution narrows and shrinks towards zero, until the voltage increase in early 2021 that causes the distribution to rebound to c.2015 levels. The red points mark the modes of the gain-corrected PI = gC + gS ·SAMP (see Equation 7.4).
images/fig_7_9_hrcsgain.png
Figure 7.9: As in Figure 7.8, for the HRC-S. The shaded distribution depicts the change in the distribution of scaled SUMAMPS over time for AR Lac observed on-axis prior to the voltage increase in early 2021. The red dots indicate the averages of the PI. Gain correction maps available in CALDB allow much of this gain decline to be mitigated when pulse invariant (PI) distributions are computed.

7.9  UV/Ion Shields

The placement, composition, and thickness of the various UV/Ion shields (filters) are shown in Figure 7.1. Details of the UVIS transmission as a function of energy can be found at https://cxc.harvard.edu/cal/Hrc/detailed_info.html#uvis_trans.
The shields suppress out-of-band (outside the X-ray band) radiation from the ultraviolet through the visible. The detector response to out-of-band light for an object in its field-of-view is a possible source of unwanted signal. Suppressing out-of-band radiation is particularly important for observing sources which have bright EUV and UV fluxes. The HRC has strongly reduced sensitivity in this spectral region, as shown in Figure 7.10. As part of the in-flight calibration program the bright A star Vega (A0V, U=0.02, B=0.03, V=0.03) was observed with both the HRC-I and HRC-S. The predicted count-rate for HRC-I was 7×10−4 cts s−1. From monitoring observations of Vega, an upper limit to the UV rate of 8 ×10−4 cts s−1 is calculated (Pease et al. 2005). The image of Vega was also placed on three regions of the HRC-S  - the inner segment "T", the thin aluminum inner segment, and on one of the thin aluminum outer segments. The predicted count-rates were 1, 400, and 2000 cts s−1 respectively. The corresponding observed rates were 0.2, 240, and 475 cts s−1. Sirius was observed with the HRC-S/LETGS to obtain a soft X-ray spectrum of Sirius B (white dwarf) and Sirius A (A1V, V=-1.46, B-V=0.01) was seen in zeroth order at about the expected count rate. Based on these sets of observations, the UV/Ion shields are performing as designed. Ongoing monitoring observations of Vega indicate no change in the UV response of HRC-I and HRC-S since launch. For a detailed discussion of the out-of-band response of the HRC to stars, see https://hea-www.harvard.edu/HRC/calib/palermopaper.ps, which allows one to determine the out-of-band count-rate produced by a blackbody source with known Teff, mV, and NH.
Scattered UV, far ultraviolet (FUV), and extreme ultraviolet (EUV) light from the Sun or the bright Earth may cause a background dependence on viewing geometry. The spacecraft was designed to limit the contribution from stray scattered radiation to 0.01 cts cm−2 s−1 (2.4×10−7 cts arcsec−2 s−1) on the HRC. The imaged components of scattered radiation are dependent on the solar cycle, but are at most  ∼  0.01 cts cm−2 s−1 for most lines of sight.
images/POG_hrc_uv.png
Figure 7.10: The HRC-I (top) and the center section of the HRC-S (bottom) UV/Ion shield effective area as a function of wavelength.

7.10  Quantum Efficiency and Effective Area

The efficiency of the HRC detector is the product of the appropriate UV/Ion shield transmission and the quantum efficiency of the CsI coated MCP. Pre-flight flat field measurements show a 10% variation in the efficiency across the HRC-I. The HRC-S also exhibits efficiency variations of the same magnitude, with the complex structure of the HRC-S UVIS contributing to the spatial variations. In-flight observations of the steady coronal source Capella show that the HRC-I variation is known to better than  ∼ 2% at high energies. There are time-dependent decreases in the QE for both HRC-I and HRC-S. The HRC-S decline is wavelength independent and amounts to  ∼ 15−20% over the course of the mission. These corrections are incorporated into the corresponding CALDB files. The HRC-I QE has been stable at short wavelengths, but has declined by  ∼ 10% at long wavelengths based on measurements of the white dwarf HZ 43. The HRC-I also shows some fluctuations at low energies at large offset locations,  ∼ 10 arcmin away from the nominal aimpoint (see https://cxc.harvard.edu/ccw/proceedings/2007/presentations/possonbrown3/).
The combined HRMA/HRC effective areas - the product of the HRMA effective area, the quantum efficiency of the HRC-I or the HRC-S and the transmission of the appropriate UV/Ion shield, integrated over the point spread function - are shown in Figure 7.11. Monitoring of the efficiency of both detectors is continuing. The charge extracted since launch has resulted in a decrease in gain in both detectors. (See https://cxc.harvard.edu/cal/Hrc/).
The HRC-S QE has been declining at an average rate of ≈ 2.4% per year. This decline has been steady, and is weakly dependent on wavelength, with higher energies affected less than lower energies. The QE decline in the HRC-I accelerated after c.2015, and reached ≈ 35% prior to the voltage increase; after the voltage increase, the QE relative to the beginning of the mission is estimated to be down ≈ 15% at soft energies and ≈ 5% at high energies. Similarly, the low-energy QE in the HRC-S is currently down 14% from launch. These effects are incorporated in the latest QE and quantum efficiency uniformity (QEU) maps in the current CALDB.
images/hrc_onaxis_ea_pog.png
Figure 7.11: The effective area of the HRMA/HRC-I (dashed line) and the central segment of the HRMA/HRC-S in imaging mode (solid line) integrated over the full PSF. Absorption edges are due to the iridium coating on the mirrors, the CsI MCP coating, and the polyimide/Al of the UVIS.

7.11  On-Orbit Background

7.11.1  HRC-I

The HRC-I anti-coincidence shield reduces the on-orbit valid event rate by about a factor of 5 to  ∼ 100-150 cts s−1 over the field; without on-board anti-coincidence vetoing the rate would greatly exceed the telemetry limit of 184 cts s−1. After standard processing, the Level 2 event file background rate is ≈ 3.5×10−5 cts s−1 arcsec−2, though variations of 20% are possible. The background varies smoothly over the field with no more than a 10% difference between the center (lower) and edges (higher) of the detector. The background is not azimuthally symmetric (see Isobe & Juda 2009). Note, the total event rate remains unchanged, but detector events in coincidence with anti-coincidence events no longer enter the telemetry data stream. Before launch the expected rate, after vetoing the effects of cosmic rays, was 10-20 cts s−1 composed of mainly the internal rate of the MCPs (10-15 cts s−1), and a small contribution from cosmic rays due to anti-coincidence shield inefficiency. The anti-coincidence shield inefficiency has increased in recent years, and the quiescent background has increased by ≈ 10%. For observations where there is a chance that the telemetry saturation limit might be hit, the HRC Instrument Team has devised a new instrument mode that excludes the events recorded in the two outermost taps from being telemetered. This mode can be selected in consultation with Chandra uplink support contact scientists when the observation is scheduled. There is additional background in the HRC-I that is not well understood. For point source detection and exposure times of 100 ks or less the background is virtually negligible. However, for extended low surface brightness objects this relatively low rate can become significant depending on the specific details of the source.
Ground-based filtering further reduces the non-X-ray background in the HRC detectors (see Murray et al. 2000, Juda et al. 2000 and Wargelin et al. 2001; https://cxc.harvard.edu/cal/Letg/Hrc_bg/). After filtering the non-X-ray background for HRC-I data is reduced by  ∼ 40% while the corresponding reduction in X-ray events is less than a few percent. For the HRC-S, the non-X-ray background is decreased by  ∼ 50% and the X-ray loss is 1−2%. Furthermore, filtering makes the spatial distribution of the detector background flatter. Filtering also removes saturated events responsible for faint secondary "ghost" images (see Section 7.12).

7.11.2  HRC-S

The anti-coincidence shield of the HRC-S does not work because of a timing error in the electronics. The error is not correctable. As a result the event rate is very high and exceeds the telemetry rate limit. To cope with this problem the HRC team has defined a "spectroscopy region" which is about 1/2 of the full width and extends along the full length of the HRC-S detector. The spectroscopy region ( ∼ 10 mm) is implemented using the edge blanking feature of the electronics. With this change, the telemetered quiescent background rate is about 120 cts s−1.
The background can be further reduced in ground data processing by using pulse height filtering that preferentially selects X-rays over cosmic ray events. A reduction in background by a factor of about three is possible for dispersed spectra. Thus there are two relevant background rates for the HRC-S: a telemetry rate of 120 cts s−1 and a post-processing rate for calculating signal-to-noise. The latter is discussed in detail in Section 9.3.6 (see especially Figure 9.22).

7.11.3  Temporally Variable Background

Both the HRC-I and HRC-S experience occasional fluctuations in the background due to charged particles. These periods of enhanced background are typically short (a few minutes to a few tens of minutes) and are anywhere from a factor of two to ten over the quiescent rates. The increased background appears to be uniformly distributed over the detector and introduces no apparent image artifacts. On average it seems that no more than about 20% of the observing time is affected by these events, and they are easily recognized in the secondary science rate data and so can be filtered out if desired. An example of this behavior is shown in Figure 7.12. See Juda et al. (2002) for more information on the HRC background.
images/bkg_rate_variability_run_2.png
Figure 7.12: An example of the background variability during a  ∼ 30 ks HRC-I observation of the supernova remnant (SNR) SNR G21.5-09 taken on 1999-Oct-25. The total event rate (middle) and valid event rate (bottom) show correlated bursts up to  ∼ 800 cts s−1. The bursts are uniformly distributed over the detector. The anti-coincidence shield (top) exhibits no correlated enhancements. The total and valid rates differ by  ∼ 200 cts s−1 due primarily to cosmic ray events that are vetoed and don't appear as valid events in the telemetry.
The background increases due to increased cosmic ray flux during solar cycle minima (see Figure 7.13). The difference between cycle minimum and maximum can be as much as a factor of two. On-orbit non-sky background spectra and events lists are available in CALDB for analysis and modeling. The spectra are obtained during yearly AR Lac observations (see Figure 7.14). A recipe for their use in filtering on PI to reduce background is described in the CIAO thread https://cxc.cfa.harvard.edu/ciao/threads/hrci_bg_spectra/. The events data sets are obtained during the times when ACIS is viewing the sky but the HRC MCP HV is at the operational level so that the HRC is sensitive to the cosmic ray flux. The data sets are event lists and can be processed and filtered the same as data from a sky observation. The datasets needed to make background images for use in constructing exposure corrected flat-field images are available in CALDB (since v4.3.0). A recipe for their use is described in the CIAO thread https://cxc.harvard.edu/ciao/threads/hrci_bg_events.
images/hrci_medianbkg_ctrt.png
Figure 7.13: The change in HRC-I background rate with time. The deadtime corrected count rate per square arcsec is shown with error bars for each HRC-I observation. The lower envelope represents the quiescent rate, and the fluctuations are due to the occasional background flaring. The HRC-S data are similar.
images/fig7_18_hrci_arlac_bkg.png
Figure 7.14: The shape of the background spectrum varies with time on both the HRC-I and HRC-S. This plot shows the spectra of both the scaled SUMAMPs (top panel) and Pulse Invariant channels (PI; bottom panel), color coded by years into the mission (red is early, blue is current). The spectral shapes are obtained from the central 8 arcmin region of the HRC-I during regular AR Lac calibration observations, with the source photons and observations affected by high background excluded. The grey shaded region represents the full envelope, and the individual curves are the smoothed spectra, normalized by total counts and rescaled to a sample maximum of 1. The white curves represent the latest observations prior to the voltage change.
Furthermore, much of the background can be alleviated by filtering out events with PI < 20 and PI > 350 on the HRC-I. The background is reduced by  ∼ 20% even as only ≈ 1−2% of the source counts are lost (see Figures 7.15 - 7.17). The CIAO thread https://cxc.harvard.edu/ciao/threads/hrci_bg_spectra/ describes how to perform this estimate for different source models background spectra. This thread can also be followed to compute background reduction factors for non-grating HRC-S sources, provided that they are extended or are observed off-axis, and user generated background spectra are used. This approach for improving signal-to-noise is not recommended for sources observed on-axis with the HRC-S, since gain near the aimpoint varies significantly on very small scales and is not well calibrated, potentially leading to undesired filtering effects. The approach should also not be used for data obtained with a grating in place; see Section 9.3.6 for a discussion of background reduction using PI filtering for dispersed spectra.
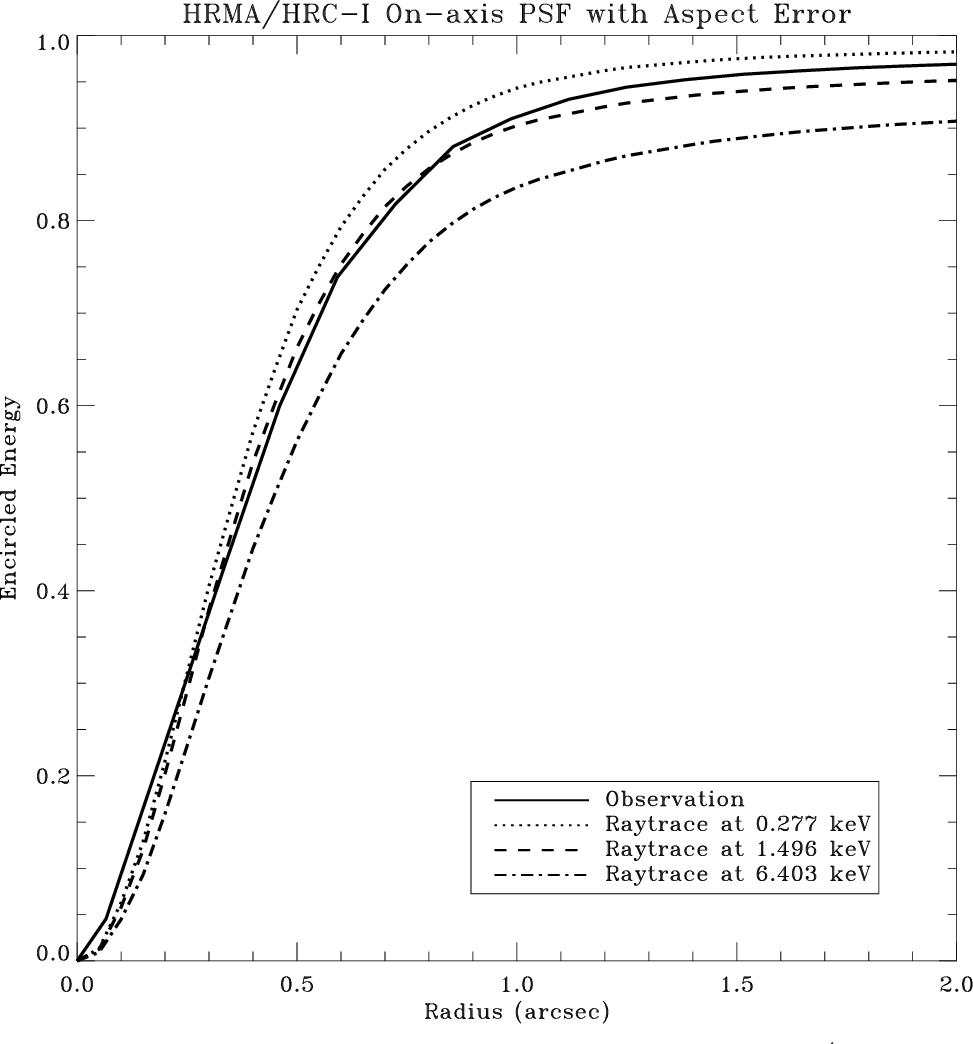
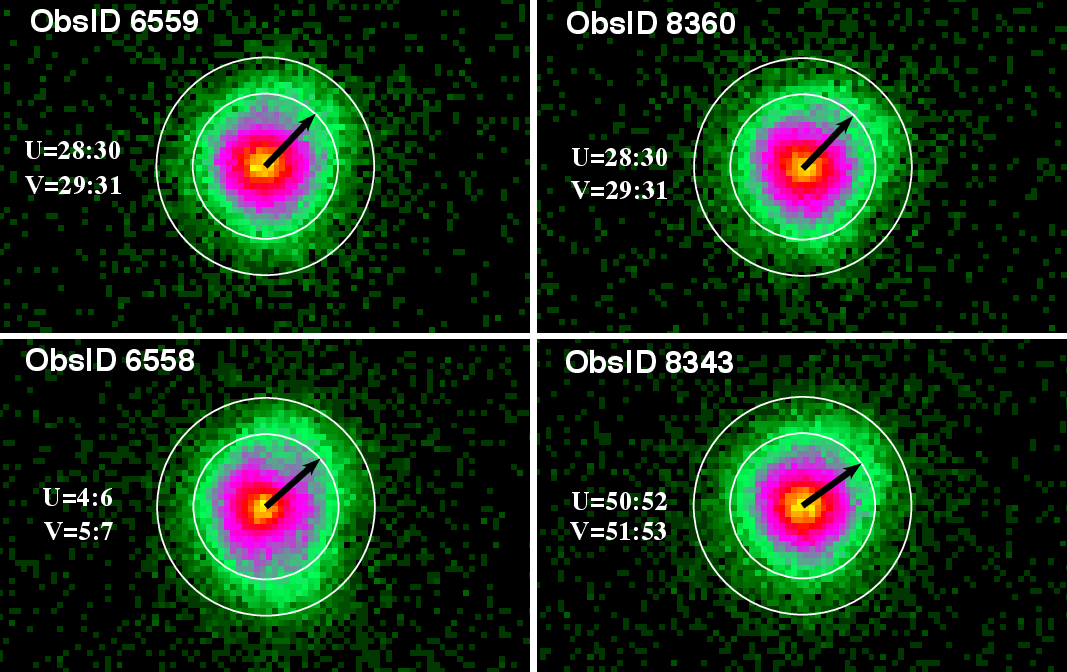
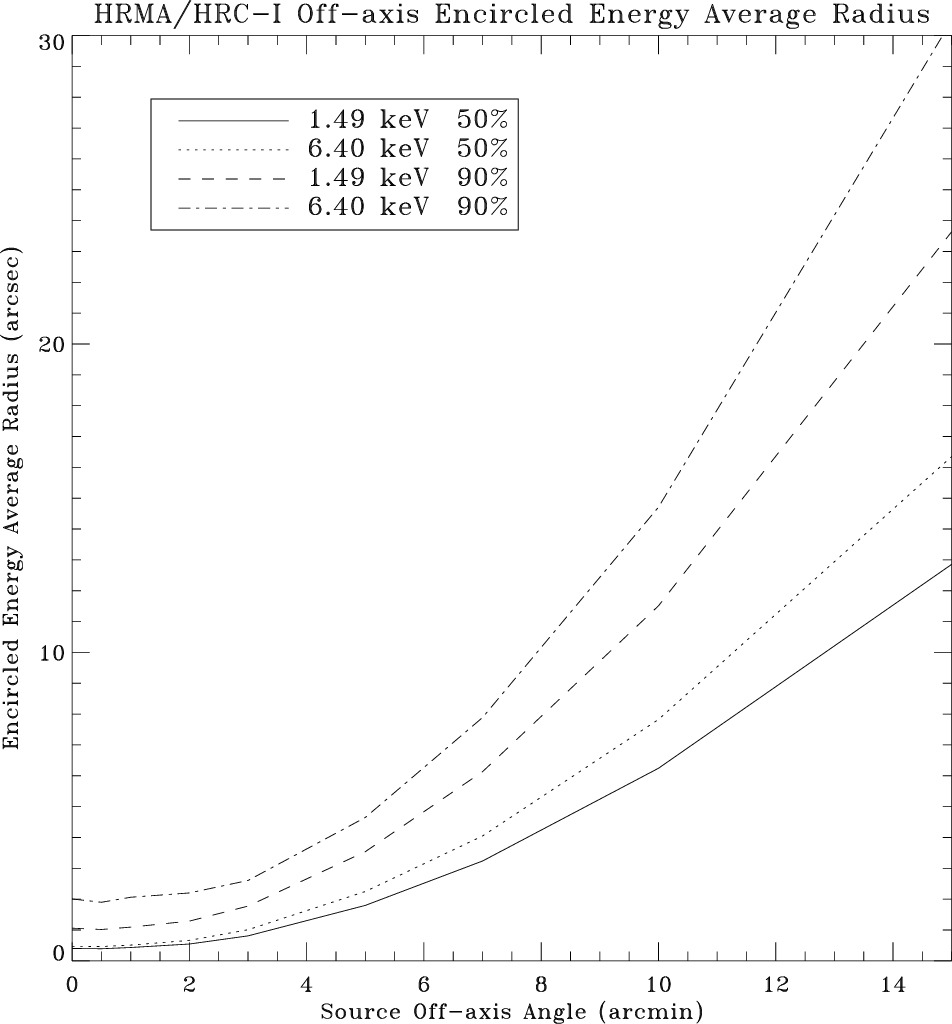
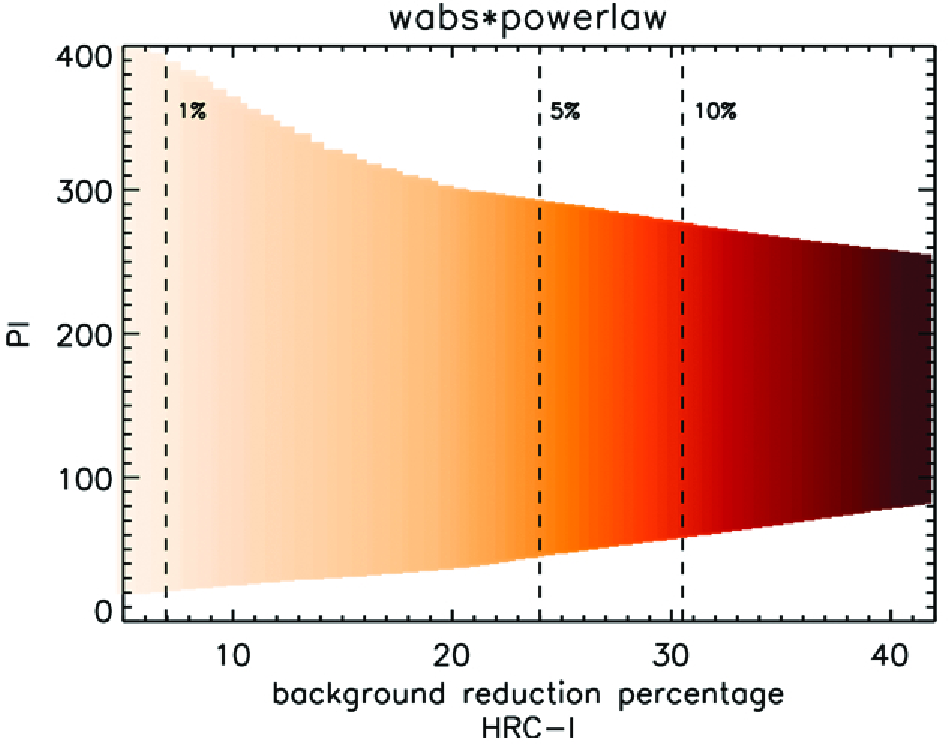
images/hrci_bgfilt_wabspow.png
Figure 7.15: An estimate of the range of PI values that should be included to reduce the background by a given percentage is shown in the figure as a shaded band for sources with absorbed power-law spectra. (see https://cxc.cfa.harvard.edu/ciao/threads/hrci_bg_spectra/). The depth of the shading indicates how much of the source events are expected to be lost. The vertical dashed lines indicate the background reduction for source event losses of 1%, 5%, and 10%. As shown in Figure 7.14, the background varies with time. Here, for the sake of definiteness, we use the background from the year 2008.
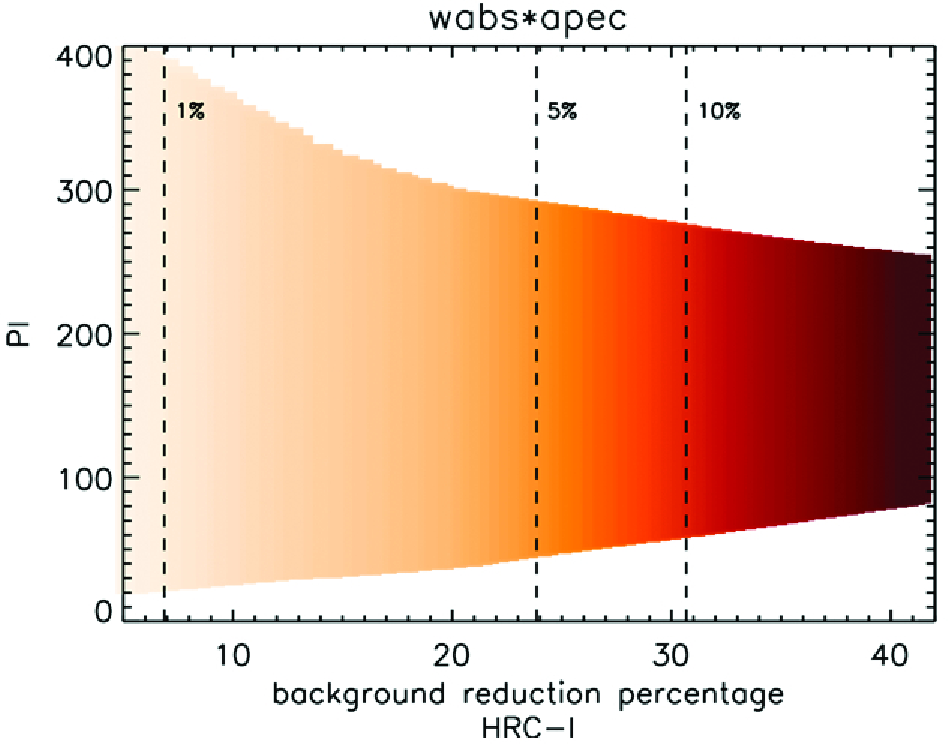
images/hrci_bgfilt_wabsapec.png
Figure 7.16: As Figure 7.15, but for sources with thermal spectra.
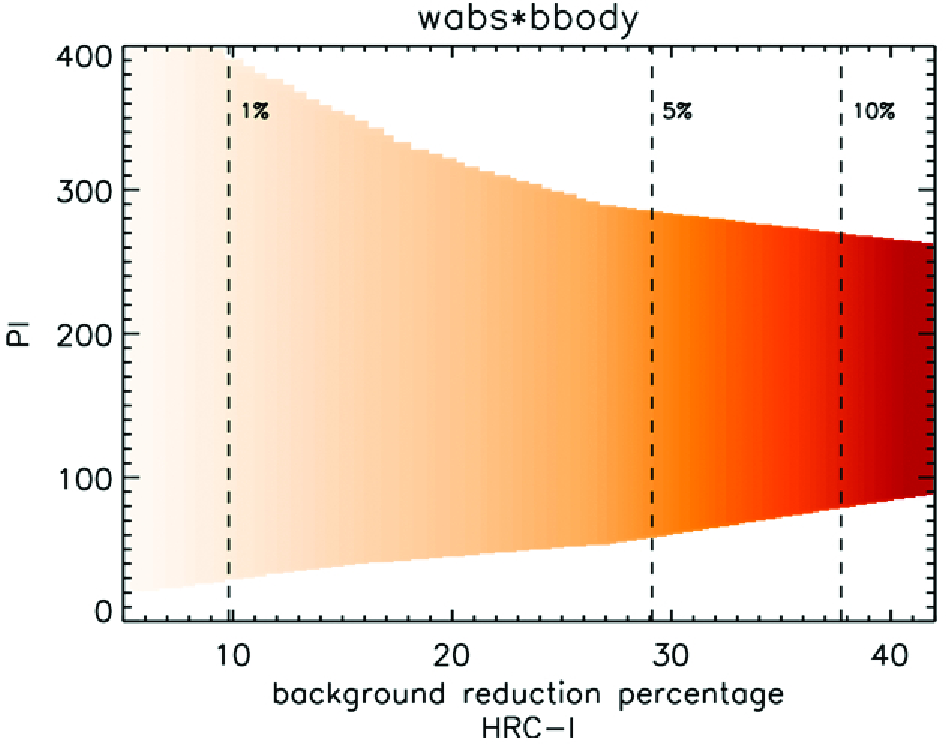
images/hrci_bgfilt_wabsbbody.png
Figure 7.17: As Figure 7.15, but for sources with blackbody spectra.

7.11.4  Limiting Sensitivity

The limiting sensitivity for the detection of a source is dependent on both the background count rate and the estimated counts from the source. In Tables 7.2 and 7.3, we compute the source counts for on-axis point sources with different spectral shapes and estimate the flux that would be detected at 3σ in a 50 ksec observation. The source counts are assumed to be collected in a circle of radius 2.6 arcsec, and the background is assumed to be collected in an area 10× larger. The source extraction radius is not optimized for source detection and is intended to provide ballpark estimates of the limiting sensitivity. For each spectral model, the counts-to-energy conversion factor is computed using effective area curves derived from recent calibration observations (ObsID 25593 for HRC-I, and ObsID 25634 for HRC-S).
Table 7.2: HRC-I sensitivity
Model
Parameters 		NH
[×1020 cm−2] 		Limiting Fluxf [×10−15 ergs s−1 cm−2] at
Background level [counts s−1 arcsec−2]
5×10−6 10−5 5×10−5 10−4
xspowerlaw
0.01 6.8 8.2 17. 27.
α = 1.4 4 8.3 10. 21. 33.
100 22. 27. 57. 89.
0.01 5.1 6.1 13. 20.
α = 1.7 4 6.1 7.3 15. 24.
100 18. 21. 45. 71.
0.01 4.0 4.8 10. 16.
α = 2.1 4 4.4 5.2 11. 17.
100 13. 16. 33. 52.
0.01 3.8 4.6 9.7 15.
α = 2.4 4 3.6 4.4 9.2 14.
100 11. 13. 27. 42.
xsapec
0.01 7.9 9.5 20. 32.
kT=0.086 keV 4 3.0 3.6 7.7 12.
100 2.0 2.4 5.0 7.8
0.01 2.0 2.4 5.0 7.8
kT=0.432 keV 4 1.8 2.2 4.6 7.2
100 2.5 3.0 6.4 10.
0.01 2.3 2.8 5.8 9.2
kT=0.862 keV 4 2.0 2.4 5.2 8.1
100 3.4 4.1 8.6 13.
0.01 3.4 4.1 8.6 13.
kT=1.72 keV 4 3.3 3.9 8.2 13.
100 6.8 8.2 17. 27.
        f: For a 3σ detection of an on-axis source in a 50 ks observation with a 2.6 arcsec-radius
source circle and background collected in an area 10× larger.
Table 7.3: HRC-S sensitivity
Model
Parameters 		NH
[×1020 cm−2] 		Limiting Fluxf [×10−15 ergs s−1 cm−2] at
Background level [counts s−1 arcsec−2]
5×10−6 10−5 5×10−5 10−4
xspowerlaw
0.01 6.7 8.1 17. 27.
α = 1.4 4 8.2 9.9 21. 33.
100 24. 29. 61. 95.
0.01 4.9 5.9 12. 19.
α = 1.7 4 6.0 7.2 15. 24.
100 19. 23. 48. 75.
0.01 3.8 4.5 9.5 15.
α = 2.1 4 4.2 5.0 11. 17.
100 14. 17. 35. 56.
0.01 3.5 4.2 8.9 14.
α = 2.4 4 3.4 4.1 8.6 13.
100 11. 14. 29. 45.
xsapec
0.01 3.5 4.2 8.9 14.
kT=0.086 keV 4 2.5 3.0 6.3 9.9
100 2.0 2.3 5.0 7.8
0.01 2.0 2.4 5.2 8.1
kT=0.432 keV 4 1.9 2.3 4.8 7.5
100 2.6 3.2 6.7 10.
0.01 2.3 2.8 5.9 9.2
kT=0.862 keV 4 2.1 2.5 5.3 8.3
100 3.5 4.2 8.9 14.
0.01 3.3 3.9 8.2 13.
kT=1.72 keV 4 3.2 3.8 8.1 13.
100 7.1 8.5 18. 28.
        f: For a 3σ detection of an on-axis source in a 50 ks observation with a 2.6 arsec-radius
source circle and background collected in an area 10× larger.

7.12  Instrument Anomalies

Power supply anomalies:   On 2022-Feb-9, the HRC instrument experienced an electronics anomaly. This was similar in characteristics to the anomaly experienced on 2020-Aug-24, when there was a drop in power being supplied to the instruments. After the 2020-Aug anomaly, the HRC was switched over to a redundant set of power supplies and command and processing electronics ("Side B"), and had been operating nominally prior to the anomaly on 2022-Feb-9. Subsequent investigations showed that the anomalies differed in detail, and that switching to the original set of power supplies and electronics ("Side A") would restore operational functionality. An attempt was made on 2022-Mar-11 to restore Side B functionality, but this was unsuccessful. The switch to Side A was made on 2022-May-19, which successfully restored the instrument functionality. Several check-out observations were carried out after that, and analysis shows no departure from known trends in instrument characteristics. The degap is unaffected, and gain and QE drops (see Sections 7.8,9.3.6) are consistent with previous trends. New thermal constraints have been added that limit observation durations to a maximum of 14.5 ks at a time, with a substantial cooling duration following each observation. HRC science observations resumed on 2023-Apr-10.
PSF "ghost":   Early observations with the HRC-I showed a faint secondary "ghost" image. This "ghost" image was a displaced, weaker ( ∼ 3%) image  ∼  10 arcsec on one side of every source in the HRC-I field of view, generally along the negative U axis of the instrument (Figure 7.1). The cause of this imaging anomaly is saturation of the fine position amplifiers. A change in the HRC-I operating high-voltage reduced the occurrence of saturating events and the previously mentioned event processing algorithms, which are now part of the CXO/HRC data pipeline, label these events and filter them out. The combination of the HV change and filtering have reduced the relative intensity of the ghost image to < 0.1 %, effectively eliminating it. If the location of the ghost image interferes with features of the source, the CIAO tool obsvis can be used to determine a roll angle that places the source features away from the ghost image. A similar ghost image existed in the HRC-S but at a much reduced intensity.
Timing Error:   The HRC has a hardware problem that corrupts the data from the position taps under a specific set of conditions: 1) the amplifier scale factor is switched to the least sensitive scale, 2) an even number of taps on the axis have signals that are above a set threshold, and 3) the event occurs on the negative side of the tap. When these conditions are met the tap signals are sampled while the amplifiers are still ringing after switching from the initial guess for the event coarse position to the correct one. The ringing results in offsets on the telemetered tap values from their true values, with the smallest signal of the triplet for an axis being most affected. When the event position is calculated from corrupted data, positions are incorrectly determined and can be off by a few pixels. This ringing is partially corrected for in ground processing (Juda et al. 2000). These corrections are implemented via the CIAO tool hrc_process_events. Observers, if they are concerned that the ringing may be producing artifacts, can apply additional filtering to remove events with AMP_SF=3.
A wiring error in the HRC causes the time of an event to be associated with the following event, which may or may not be telemetered. The result is an error in HRC event timing that degrades accuracy from about 16 microsec to roughly the mean time between events. For example, if the trigger rate is 250 events/sec, then the average uncertainty in any time tag is less than 4 millisec.
The HRC team has developed a special operating mode that allows high precision timing to be achieved (see Section 7.15.1). This timing mode uses only the central segment of the HRC-S. Disabling the outer two segments lowers the total count-rate by two-thirds, dropping it below the telemetry saturation limit for most sources. Thus, there is a high probability that all events will be telemetered. In this case, once the time tag of each event has been appropriately shifted in ground processing, the original timing accuracy (16 microsec) can be recovered. When using this approach, it is prudent to be sure that the total count-rate (source plus background) is below the telemetry saturation limit to avoid telemetry saturation due to statistical fluctuations in the count-rate. Note also that due to the gain drop in both the HRC-I and the HRC-S, a large number of events will fall below the lower-level discriminator set for this mode, which could reduce the source count rate by as much as 45%. Observers should consult the Instrument or Calibration Teams if their program requires the use of this special mode.
Saturation Effects:   In addition to the primary science data for individual events, the rate of microchannel plate triggers (total rate) and triggers that pass on-board validity tests (valid rate) are telemetered to the ground. The valid rate is used to correct the primary rate for deadtime and telemetry saturation effects. As long as the primary rate is below saturation, the primary rate itself can be used to make the small ( < 1%) correction, since the event processing dead-time is known. However, when the event rate exceeds saturation, a fairly common occurrence because of background flaring from low energy protons, the valid rate is necessary to correct the event rate. Unfortunately, the total and valid event rates are overestimated by about 15% for normal operation of the HRC-S. This problem is caused by an overshoot in occasional large trigger pulses, resulting in double counting in the total and valid event on-board scalers. The primary science event is not affected, since once event processing starts with the initial trigger pulse, a gate rejects further pulses until processing is complete. The HRC-I does not have this overshoot problem. The HRC-S valid event rate is corrected in standard processing, using the fraction of event pulse amplitudes that are above a given (segment dependent) threshold.
Tailgating:   The HRC PSF also suffers from a tailgating effect, where photons within the area of the PSF that are recorded rapidly after a previous photon have less accurate positions, leading to the PSF for these events being puffier (Juda 2012, https://cxc.cfa.harvard.edu/contrib/juda/memos/hrc_pileup/index.html). Photons with arrival time differences of < 0.05 sec are affected.
Secondary Science Corruption:   Sometimes the processed data may appear to have a large number of Good Time Intervals ( >> 20) despite the full-chip background rate not showing any evidence of telemetry saturation. This is caused by a byte-shift anomaly in the secondary housekeeping files. Observers should note that the science data are not corrupted in any way, and are still available in the level 1 events list. All the events lost to time filtering may be recovered by simply not including the affected intervals in the time filtering step recommended during reprocessing. A new deadtime factor should be computed using the CIAO tool hrc_dtfstats as described in the thread Computing Average HRC Dead Time Corrections (https://cxc.cfa.harvard.edu/ciao/threads/hrc_dtfstats/).

7.13  Calibration

Calibration of the HRC included laboratory calibrations, a system-level ground calibration with the HRMA and HRC at the X-ray Calibration Facility (XRCF) at MSFC, and on-orbit calibration using celestial X-ray sources. The on-orbit calibration of the HRC is an on-going activity. See Tables 7.4,7.5 for a list of HRC calibration targets. All calibration analysis is described in detail at (https://cxc.harvard.edu/cal/Hrc).
Table 7.4: Current and past HRC-I calibration targets
Target Frequency
(per Cycle) 		Cycle Grating Purpose
2REJ1032+532 11 1 LETG/None PSF calibration
31 Com 1 > 8 None ACIS undercover; off-axis PSF & gain uniformity
3C273 1 1 None Cross-calibration with ACIS 
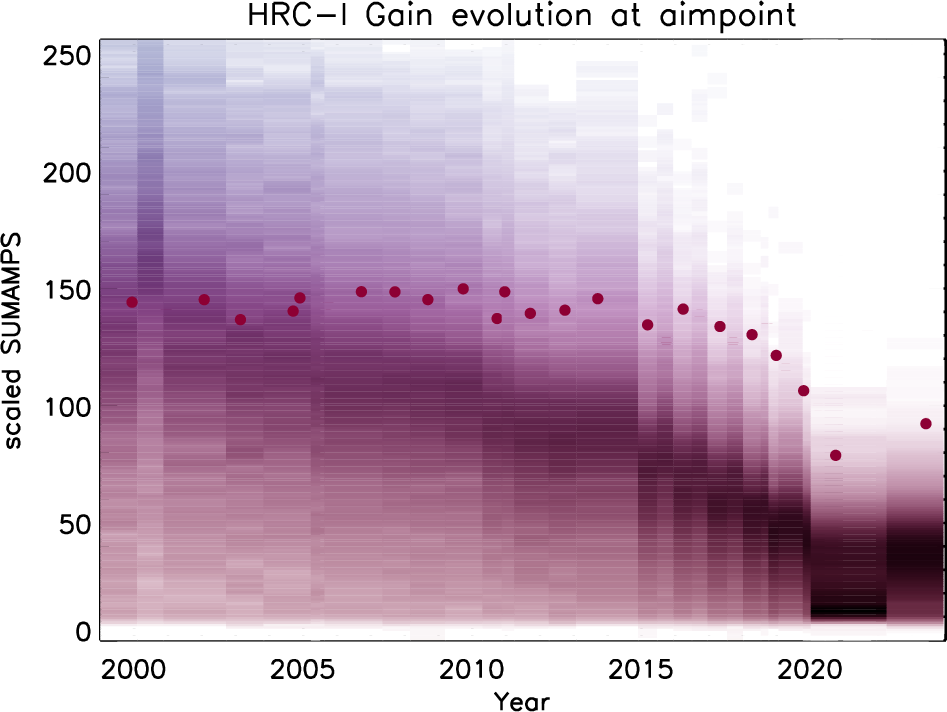
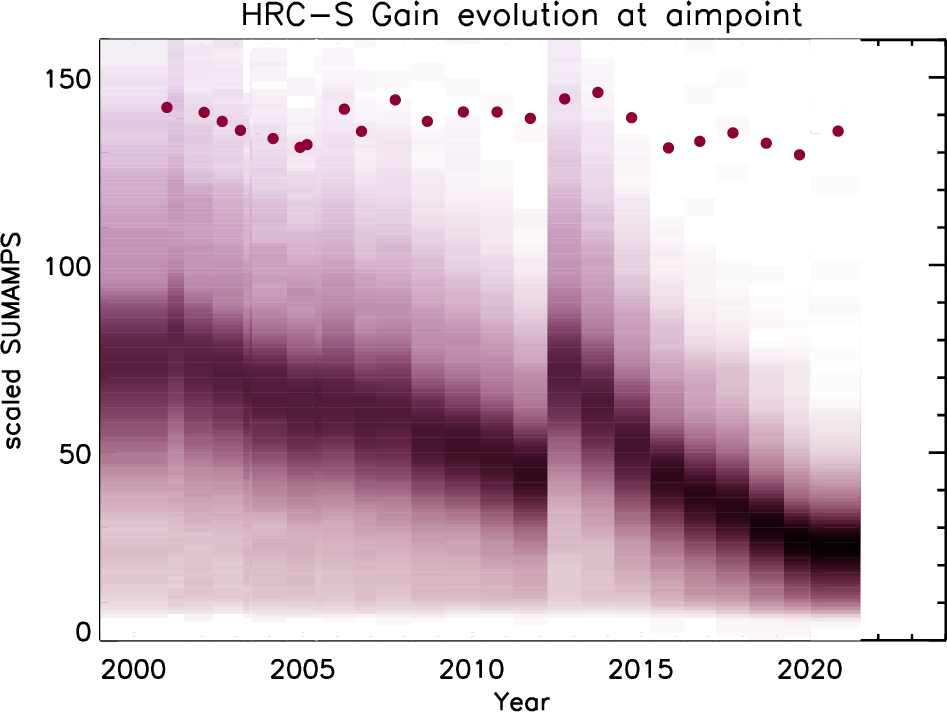
AR Lac 21 1-19 None Monitor gain at aimpoint & 20 offset locations
AR Lac 42 20+ None Monitor gain and optical axis at aimpoint & 40 offset locations
Betelgeuse 1 3-6 None Monitor UV/Ion Shield
Capella 20 7-8 None Improve de-gap corrections
Cen A 3 1 None imaging capabilities
Cas A 2 1-8 None Monitor QE; cross-calibration
Cas A 1/2 8-11 None Monitor QE; cross-calibration
Cas A 1 22 None Monitor degap
Coma Cluster 4 1None Monitor temporal variations & calibrate de-gap
Coma Cluster 1 2,3,16 None Monitor temporal variations & calibrate de-gap
E0102-72.3 1 1,14 None Cross-calibration with ACIS 
G21.5-0.9 15-8,19+ None Monitor QE; cross-calibration
G21.5-0.9 22-4 None Monitor QE; cross-calibration
G21.5-0.9 3 0-1 None Monitor QE; cross-calibration
G21.5-0.9 0.5 9-18 None Monitor QE; cross-calibration
HR 1099 7 20 None Monitor PSF size
HR 1099 1 21 None Monitor PSF size
HR 1099 1 21 HETG Monitor PSF size, calibrate 0th order and
HETGS+HRC-I configuration
HR 1099 63 1 LETG/None PSF and Wavelength calibration
HR 1099 30 20 None PSF calibration
HZ 43 1 8-15 LETGMonitor low energy response
HZ 43 2 4-7,16+ LETGMonitor low energy response
HZ 43 3 1 LETGMonitor low energy response
HZ 43 4 2-3 LETGMonitor low energy response
LMC X-1 16 1 None PSF calibration
M82 1 1 None detector imaging
N132D 2 1 None Cross-calibration with ACIS 
NGC 2516 31 None Boresighting & plate scale
NGC 2516 1 2 None Boresighting & plate scale
PKS2155-304 22LETG Monitor low energy QE; cross-calibration
PKS2155-304 1 4 LETG Monitor low energy QE; cross-calibration
Procyon 1 4-5 None ACIS undercover; off-axis PSF & gain uniformity
Proxima Cen 2 14,17 None ACIS undercover; off-axis PSF & gain uniformity
PSRB0540-69 5 1 None Verification of fast timing capability
Ross 154 1 8 None ACIS undercover; off-axis PSF & gain uniformity
RT Cru 1 14 None PSF calibration
RXJ1856.5-3754 2 4-7 None ACIS undercover; off-axis PSF & gain uniformity
Vega 21-7None Monitor UV/Ion Shield
Vega 4 7-11 None Monitor UV/Ion Shield
Vega 1 > 11 None Monitor UV/Ion Shield
Vela SNR 1 3 None low energy QE uniformity
Vela SNR 2 4 None low energy QE uniformity
Table 7.5: Current and past HRC-S calibration targets
Target Frequency
(per Cycle)		Cycle Grating Purpose
3C273 11LETGCross-calibration
3C273 1 3 LETGCross-calibration
AR Lac 2x21 3,5-8 None Monitor gain at aimpoint & 20 offset locations
AR Lac 21 1-2,4,9-19 None Monitor gain & 20 offset locations
AR Lac 1 20+ None Monitor gain and PSF at aimpoint
AR Lac 7 20 None Monitor PSF in cross-dispersion direction
Betelgeuse 41-6None Monitor UV/Ion Shield
Betelgeuse 2 7 None Monitor UV/Ion Shield
Capella 10 1 LETGMonitor gratings
Capella 1 1-7,10-13,17+ LETGMonitor gratings
Cas A 5 1 None Cross-calibrate HRC MCPs
Cas A 1/2 > 9 None Cross-calibrate HRC MCPs
G21.5-0.9 1 5-8,15,19 None Monitor QE; cross-calibration
G21.5-0.9 2 2,4 None Monitor QE; cross-calibration
G21.5-0.9 3 0,3 None Monitor QE; cross-calibration
G21.5-0.9 7 1 None Monitor QE; cross-calibration
G21.5-0.9 1 24 LETG Monitor QE; cross-calibration
HR 1099 1,21 1 LETG Wavelength calibration
HZ 43 1 8,10-12,14-15 LETGMonitor low energy response
HZ 43 2 0-7,20+ LETGMonitor low energy response
HZ 43 3 13,19 LETGMonitor low energy response
HZ 43 4 18 LETGMonitor low energy response
HZ 43 14 14 None Monitor gain across the detector
HZ 43 16 20 None Monitor gain across detector, locate thin/thick filter transition
LMC X-1 26 1 None PSF calibration
Mkn 421 1 8 LETGMonitor ACIS contamination, cross-calibration
NGC 2516 1 1 None Boresight and plate-scale
PKS2155-304 11-4 LETGGratings calibration, monitor ACIS contamination
PKS2155-304 2 4-8 LETGGratings calibration, monitor ACIS contamination
Procyon 3 1 LETGGratings calibration, cross-calibration
PSRB0540-69 7 1 None Verification of fast timing capability
PSRB1821-24 1 7 None Timing calibration
Sirius B 3 1 LETGCalibrate LETG low-energy QE
Vega 2x4 1-6 None Monitor UV/Ion Shield
Vega 4x4 6-11 None Monitor UV/Ion Shield
Vega 1x4 > 11 None Monitor UV/Ion Shield
var. blank sky ≈ 8 22+ None Background monitoring at aimpoint during cold
ECS pointings

7.14  Operational Considerations and Constraints

In addition to the general Chandra observatory level constraints (Chapter 3), there are a few HRC-specific considerations and constraints that must be taken into account when planning an observation.

7.14.1  Total Count Limits

Both the gain and the quantum efficiency are adversely affected by the total amount of charge extracted from the MCP at the point of extraction. To minimize such effects, the high voltage on the detector is lowered during passage through the radiation belts and at times of very high particle radiation. To limit the impact from X-ray sources themselves, a 450,000 count limit, per source, distributed over the dither pattern from an on-axis source at a given aimpoint has been imposed. (Any source with flux approaching the vicinity of 10−10 ergs cm−2 s−1 should be checked.) Users anticipating to exceed this count limit should so note in the comments section of the CPS form when submitting their proposal. In this case, the CXC will establish new aimpoints as necessary. Offsets in the pointing may be imposed, if necessary, to limit the accumulated dose to a given region of the MCP.

7.14.2  Count-Rate Limits

There are two count-rate limits:

Telemetry Limit

The maximum telemetered count-rate is 184 cts s−1. This is a limitation on the total count-rate received over the full field-of-view rather than for one individual source within the field. It is possible to exceed this limit and to subsequently correct the total count-rate by using the secondary science rates, which keep track of the actual detected rate, to determine the deadtime correction (see Section 7.12). The resulting deadtime fraction increases rapidly with valid event rates above 184 cts s−1. For example, at 200 cts s−1 the deadtime fraction is 8%, at 250 cts s−1 26%, and at 300 cts s−1 39%. Listed below are some methods for dealing with situations where the telemetry limit is exceeded.
  1. Bright target:
  2. Bright nearby source
There are of course, other combinations and situations that can lead to telemetry saturation - numerous faint sources on the field, a too-bright extended source, etc.

Linearity limit

During ground calibration, the HRC-I was verified to be linear for incident photon rates at  ∼ 2 cts s−1 pore−1, which translates to  ∼ 5 cts s−1 for an on-axis point source (see Kenter et al. 1997, Figure 7). The HRC-S was found to be linear for rates five times greater. At much higher incident fluxes, the measured rate will be lower than expected (see Pease & Donnelly 1998; https://cxc.harvard.edu/cal/Hrc/detailed_info.html#ctrt_lin). Observations of the coronal point source Capella with the HRC-I show that the data are consistent with the nominal correction for a point source of intensity  ∼ 19−22 cts s−1.
It is important to be aware that avoiding telemetry saturation does not guarantee that linearity limits are not exceeded. There are only three approaches to assure that the linearity limit is not exceeded:
Note that sources with high count-rates will also have smaller photon arrival time differences, which will cause the PSF to be broader (see Section 7.6).

7.15  Observing with HRC - Operating Modes

For many observations, it is only necessary to specify the instrument, the exposure time, and the target coordinates. However, there are a number of optional parameters that might be invoked to optimize a particular observation. Tools such as PIMMS and MARX can be used to plan an observation, e.g., to account for the background when estimating sensitivity. These tools may be found at https://cxc.harvard.edu/proposer/.

7.15.1  Timing Mode

The HRC-S is normally operated in spectroscopy mode, where signals from any of the three MCP segments can be recognized as triggers. An alternate mode of operation (timing) ties the signals from the outer segments to ground so that only signals from the center MCP generate triggers. A key distinction of this mode from using an edge-blanked region (described below) to select only the center MCP segment is that the timing mode selects events without using the on-board veto logic. This preferred method of doing high-precision timing observations reduces the active detector area, minimizing the total trigger rate. Provided that this rate is below telemetry saturation, all events will then be telemetered and the event time tags can be correctly assigned in ground processing (see Section 7.12).
The HRC-S, when used in this mode, provides about a 6 x 30 arcmin field of view.

7.15.2  Edge and Center Blanking

It is possible to define a rectangular region, other than the default region, on both the HRC-I and the HRC-S. Events from either inside (edge-blanking) or outside (center-blanking) the defined regions are telemetered. This could be done, for example, to prevent events from a nearby bright source from contributing to telemetry (see Section 7.14.2). If a proposer wishes to define such a rectangular region, they should state this request in the "Remarks" field of the CPS form to prompt discussions with a CXC Support Scientist.

7.16  References

General

David, L.P., Harnden, F.R. Jr., Kearns, K.E, and Zombeck, M.V., The ROSAT High Resolution Imager (HRI) Calibration Report, revised (1999).
https://hea-www.harvard.edu/rosat/hricalrep.html
Drake, J.J., Kashyap, V.L., Wargelin, B.J., and Wolk, S.J., Pointing Chandra toward the Extreme Ultraviolet Fluxes of Very Low Mass Stars (2020), ApJ, 893, 137.
Fraser, G., "X-ray Detectors in Astronomy", 1989, Cambridge University Press.
Giacconi, R., et al., 1979, Ap. J., 230, 540.
Murray, S.S., Chappell, J.H., Elvis, M.S., Forman, W.R., Grindlay, J.E., Harnden, F.R., Jones, C.F., Maccacaro, T., Tananbaum, H.D., Vaiana, G.S., Pounds, K.A., Fraser, G.W., and Henry, J.P., "The AXAF High Resolution Camera (HRC) and its use for observations of Distant Clusters of galaxies" Astro. Lett. Comm., 26, 113-125, 1987.
Murray, S.S., et al., "In-flight Performance of the Chandra High Resolution Camera", SPIE, 4012, 2000. https://cxc.cfa.harvard.edu/cda/SPIE/smurray2000.pdf
Zhao, P., 2014, CXC Memo, Nov 1 2014, Chandra Optical Axis, Aimpoint and Their Drifts The optical axis of the HRC-I is currently measured to be at (ChipX,ChipY)=(7586.7±14.2, 7741.8±4.7), and that of the HRC-S is at (ChipX,ChipY)=(2194.6±10.6,8913.4±10.6) (§ 4.5.5).
Zombeck, M.V., Chappell, J. H , Kenter, A, Moore, R., W., Murray, S. S., Fraser, G.W., Serio, S.,"The High Resolution Camera (HRC) on the Advanced X-ray Astrophysics Facility (AXAF)", Proc. SPIE, 2518, 96, 1995.

Position modeling, de-gap corrections, and event screening

Juda, M., et al., "Improving Chandra High Resolution Camera event positions via corrections to cross-grid charge detector signals", SPIE Proceedings, 4140, 2000. https://cxc.cfa.harvard.edu/contrib/juda/memos/spie2000_tap_correction.html
Juda, M., & Karovska, M., "Chandra's Ultimate Angular Resolution: Studies of the HRC-I Point Spread Function", AAS/HEAD 2010. https://hea-www.harvard.edu/ juda/memos/HEAD2010/HEAD2010_poster.html
Karovska, M., 2011, "Followup Study of the PSF Asymmetry", CXC Memo, 2011-Jun.
Kashyap, V., "Analysis of Chandra PSF feature using ACIS data", CXC Memo, 2010-Oct. https://cxc.harvard.edu/cal/Hrc/PSF/acis_psf_2010oct.html
Kashyap, V., et al., 2005, "HRC-S Degap Corrections".
https://cxc.harvard.edu/cal/Letg/Hrc_disp/degap.html
Kenter, A., "Degap as a Transformation of Probability Distribution Problem", 1999-Mar-01. https://cxc.harvard.edu/cal/Hrc/Documents/degap.pdf
Murray, S.S., Chappell, J.H., 1989, SPIE 1159, 460-475. "Position Modeling for the AXAF High resolution Camera (HRC)"
Murray, S.S., et al., "Event Screening for the Chandra X-ray Observatory High Resolution Camera (HRC)", SPIE Proceedings, 4140, 2000.
https://cxc.harvard.edu/cda/SPIE/smurray2000b.pdf
https://cxc.harvard.edu/ciao/caveats/psf_artifact.html (CIAO Caveats page on the PSF Artifact)

Count-rate limitations and linearity

Juda, M and Dobrzycki, A, "HRC Deadtime and Telemetry Saturation", 1999-Jun-18.
https://cxc.harvard.edu/contrib/juda/memos/tlm_sat.html
Juda, M., "Telemetered vs. Processed Events", memo, 2001-Dec-07.
https://cxc.harvard.edu/contrib/juda/memos/proc2valid/index.html
Juda, M., "HRC-S Double Pulse Fraction", memo, 2002-Jun-27.
https://cxc.harvard.edu/contrib/juda/memos/proc2valid/pha_fraction.html
Kenter, A.T., Chappell, J.H. Kobayashi,K.,Kraft,R.P., Meehan, G.R., Murray, S.S., Zombeck, M.V., Fraser, G.W., Pearson, J.F., Lees, J.E., Brunton, A.N. and Pearce, S.E. Barbera, M., Collura, A., Serio, S., "Performance and Calibration of the AXAF High Resolution Camera I " SPIE 3114, 1997.
Pease, D.P., & Donnelly, H., memo, 1998-May.
https://cxc.harvard.edu/cal/Hrc/detailed_info.html#ctrt_lin
Zombeck, M. V., "Secondary Science Rate Double Counting", memo, 2002-Dec-02.
https://hea-www.harvard.edu/HRC/calib/doublecount.html

Calibration

https://cxc.harvard.edu/cal (CXC calibration site)
https://hea-www.harvard.edu/HRC/calib/calib.html (HRC IPI Team calibration site)
https://cxc.harvard.edu/cal/Hrc/(HRC CXC Cal team site)
Juda, M., 2012, CXC Memo, "Pile-up" Effect on the HRC PSF
https://cxc.cfa.harvard.edu/contrib/juda/memos/hrc_pileup/index.html
Kenter, A.T., Chappell, J., Kobayashi, K., Kraft, R.P., Meehan, G.R., Murray, S.S., Zombeck, M.V., "Performance and Calibration of the AXAF High Resolution Camera: I. Imaging Readout", SPIE, 3114, 26, 1997.
https://cxc.cfa.harvard.edu/cal/spie/spie97_kenter.pdf
Kenter, A., et al., "In-flight Performance and Calibration of the Chandra High Resolution Camera Spectroscopic Readout (HRC-I)" SPIE, 4012, 2000.
https://hea-www.harvard.edu/HRC/calib/hrci.spie2000.ps
Kraft, R.P., Chappell, J., Kenter, A.T., Kobayashi, K., Meehan, G.R., Murray, S.S., Zombeck, M.V., "Performance and Calibration of the AXAF High Resolution Camera: II. the Spectroscopic Detector", SPIE, 3114, 53, 1997.
https://hea-www.harvard.edu/HRC/calib/spie97_kraft.ps
Kraft, R., et al., "In-flight Performance and Calibration of the Chandra High Resolution Camera Spectroscopic Readout (HRC-S)" SPIE, 4012, 2000.
https://cxc.harvard.edu/cda/SPIE/kraft2000.pdf
Meehan, G.R., Murray, S.S. , Zombeck, M.V., Kraft, R.P., Kobayashi, K., Chappell, J.H., and. Kenter, A.T., "Calibration of the UV/Ion Shields for the AXAF High Resolution Camera", SPIE, 3114, 74, 1997.
https://hea-www.harvard.edu/HRC/calib/spie97_meehan.ps
Meehan, G, "Calibration of the HRC-I UV/Ion Shield", 1999-Oct-13.
https://hea-www.harvard.edu/HRC/calib/hrci_cal_report.ps
Meehan, G.,"Calibration of the HRC-S UV/Ion Shields", 1999-Oct-13.
https://hea-www.harvard.edu/HRC/calib/hrcs_cal_report.ps
Murray, S.M., et al., "HRC Ground Calibration Revision A”, SAO-HRC-CR-98-345, 1998, https://hea-www.harvard.edu/HRC/calib/hrccalib_a_180998.ps
Murray, S. S.; Chappell, J.H.; Kenter, A. T.; Kobayashi, K.; Kraft, R. P.; Meehan, G. R.; Zombeck, M. V.; Fraser, G. W.; Pearson, J. F.; Lees, J. E.; Brunton, A. N.; Pearce, S, E.; Barbera, M.; Collura, A.; Serio, S., "AXAF High-Resolution Camera (HRC): calibration and recalibration at XRCF and beyond", SPIE, 3114, 11, 1997.

Background

Isobe, T., and Juda, M., memo, 2007-Sep-11.
https://cxc.harvard.edu/contrib/cxchrc/Stowed_study/hrc_stowed_position_study.html
Isobe, T., and Juda, M., 2007, "High Resolution Camera Stowed Background Study", Proc. of Chandra Calibration Workshop, October 2007, Huntsville, AL.
https://cxc.harvard.edu/ccw/proceedings/07_proc/presentations/isobe/
Isobe, T., and Juda, M., 2009, "How to Create a Background Map for an Observation", memo, 2009-Jan-27.
https://cxc.harvard.edu/contrib/cxchrc/Stowed_study/hrci_image_correction.html
Isobe, T., and Juda, M., 2009, "How to Create a Background Map for an Observation", Proc. of Chandra Calibration Review, September 2009, Boston, MA.
https://cxc.harvard.edu/ccr/proceedings/09_proc/presentations/isobe/
Juda, M., "Time History of the HRC Background", memo, 2001-May-22.
https://cxc.harvard.edu/contrib/juda/memos/hrc_bkg/time_history.html
Juda, M., "HRC Rates and High Solar Activity", memo, 2001-May-21.
https://cxc.harvard.edu/contrib/juda/memos/hrc_bkg/high_solar.html
Juda, M., et al., "Characteristics of the On-Orbit Background of the Chandra X-ray Observatory High Resolution Camera", Proc. SPIE 4851, August 2002
https://cxc.harvard.edu/contrib/juda/memos/spie2002/spie2002.html,

Detector coordinate systems

McDowell, J., "Coordinate Systems for Analysis of On-orbit Chandra Data, Paper I: Imaging", https://cxc.harvard.edu/contrib/jcm/ncoords.ps

Counts lifetime

Kenter, A.T., K.A. Flanagan, G. Meehan, S.S. Murray, M.V. Zombeck, G.W. Fraser, J.F. Pearson, J.E. Lees, A.N. Brunton, and S.E. Pearce, "Microchannel plate testing and evaluation for the AXAF high resolution camera (HRC)", Proc. SPIE, 2518, 356, 1995.

Gain, spectral response, out-of-band response

McEntee, S.C., Jackman, C.M., Weigt, D.M., Dunn, W.R., Kashyap, V., Kraft, R., Louis, C.K., Branduardi-Raymont, G., Gladstone, G.R., & Gallagher, P.T., 2022, "Comparing Jupiter's equatorial X-ray emissions with solar X-ray flux over 19 years of the Chandra mission", JGR Space Physics, 127, e2022JA030971
Kashyap, V. Posson-Brown, J., 2009, "The Imaging and Spectral Performance of the HRC", Chandra Calibration Review, 2009.14,
https://cxc.harvard.edu/ccr/proceedings/09_proc/presentations/kashyap/
Kashyap, V., Posson-Brown, J., 2005, "Spectral Response of the HRC-I", Chandra Calibration Workshop, 2005-Oct-31 to 2005-Nov-01,
https://cxc.harvard.edu/ccw/proceedings/05_proc/presentations/kashyap2/
Pease, D.O., Drake, J.J., & Kashyap, V.L., 2005, "The Darkest Bright Star: Chandra X-Ray Observations of Vega", ApJ, 636, 426
Pease, D., Kashyap, V., Drake, J., Juda, M., 2005, "Monitoring the HRC-S UV Rate: Observations of Vega", CXC Memo, 2005-May,
https://cxc.cfa.harvard.edu/cal/Hrc/Documents/hrcs_vega_uv05.pdf
Posson-Brown, J., Kashyap, V., 2005, "Monitoring the Optical/UV Transmission of the HRC with Betelgeuse", CXC Memo, 2005-Jun,
https://cxc.harvard.edu/cal/Hrc/Documents/betelgeuse.pdf
Posson-Brown, J., Kashyap, V., 2005, "Monitoring the Optical/UV Transmission of the HRC with Betelgeuse", Chandra Calibration Workshop, 2005-Oct-31 to 2005-Nov-01,
https://cxc.harvard.edu/ccw/proceedings/05_proc/presentations/possonbrown/
Posson-Brown, J., Kashyap, V., 2009, "SUMAMPS-based gain maps and RMF for the HRC-I", Chandra Calibration Review, 2009.16,
https://cxc.harvard.edu/ccr/proceedings/09_proc/presentations/possonbrown2/
Wargelin, B., 2012, CXC Memo, HRC-S Voltage Change,
https://cxc.cfa.harvard.edu/cal/Letg/newHRCShv/
Wilton, C., Posson-Brown, J., Juda, M., Kashyap, V., 2005, "The HRC-I Gain Map", Chandra Calibration Workshop, 2005-Oct-31 to 2005-Nov-01 ,
https://cxc.harvard.edu/ccw/proceedings/05_proc/presentations/wilton/
Zombeck, M.V., "HRC-I out of band response."
https://hea-www.harvard.edu/HRC/calib/hrci_cal.html
Zombeck, M.V., "HRC-S out of band response."
https://hea-www.harvard.edu/HRC/calib/hrcs_cal.html
Zombeck, M.V., et al., "Vega calibration observations."
https://hea-www.harvard.edu/HRC/calib/vega/vega.html
Zombeck, M.V., et al., "The Out-of-band Responses of the HRC on Chandra", X-ray 2000 Proceedings, Palermo, 2000.
https://hea-www.harvard.edu/HRC/calib/palermopaper.ps
Zombeck, M. V., "Response of the HRC to Vega", memo, 2002-Oct-28.
https://hea-www.harvard.edu/HRC/calib/vega/vega_trend.html
PREVIOUS INDEX NEXT