CalDB 4.9.6 Public Release Notes

I. INTRODUCTION

CalDB 4.9.6 is an upgrade to the Chandra CalDB, which includes the following items:

• ACIS T_GAIN Epochs 85+86
• HRC-S T_GMAPs N0004; PI Region Filter Cut-off
• HRC-S QE N0016 & QEU N0015 File Sets
• HRC-I QE N0013 File Set
• HRC-S GTI_LIM, T_GMAP Header Mods for Mismatched HV OBS_IDs

For the CIAO 4.13 / CalDB 4.9.6 release notes see How CalDB 4.9.6 Affects Your Analysis.

II. SUMMARY OF CHANGES

A. ACIS T_GAIN Epochs 85+86

Location:	$CALDB/data/chandra/acis/t_gain/
Filenames:	acisD2020-11-01t_gainN0008B.fits   83+84 finalized   GRADED acisD2020-11-01t_gainN0008.fits   83+84 finalized   non-GRADED acisD2021-05-02t_gainN0002.fits   85+86 provisional   GRADED acisD2021-05-02t_gain_biN0002.fits   85+86 provisional   non-GRADED

The ACIS Calibration Team has generated time-dependent gain (T_GAIN) corrections from onboard External Calibration Source (ECS) data taken during the period of 01 February 2021 through 31 July 2021 (Epochs 85+86). With this release it is now possible to finalize the T_GAIN for the previous bi-epochal period (Epochs 83+84, August 2020 through January 2021). These updates are included in the files above with effecive dates 2021-05-02T12:00:00 (provisional) and 2020-11-01T00:00:00 (finalized) respectively.

This release affects all ACIS observations taken since 2020-11-01T00:00:00, and users of any OBS_IDs with DATE-OBS later than that date are encouraged to reprocess their datasets. The degree of the corrections is similar to those of previous T_GAIN releases, and those analyzing narrow line-source data are the most likely to be affected signficantly. See the Section III.a technical details section below for further information regarding these specific file upgrades.

See the ACIS Time-dependent Gain why page for a more basic explanation of the time-dependent gain correction.

PIPELINES/TOOLS AFFECTED:

ACIS Level 1 pipeline tool acis_process_events.

CIAO script chandra_repro uses acis_process_events to reprocess ACIS observation data.

THREADS AFFECTED:

Reprocessing Data to Create a New Level=2 Event File

B. HRC-S T_GMAPs N0004; PI Region Filter Cut-off

Location:	$CALDB/data/chandra/hrc/t_gmap/
Filenames:	hrcsD1999-07-22t_gmapN0004.fits hrcsD2012-03-29t_gmapN0004.fits

Location:	$CALDB/data/chandra/hrc/tgpimask2/
Filenames:	letgD1999-07-22pireg_tgmap_N0001.fits letgD1999-07-22pireg_tgmap_N0002.fits

The LETGS calibration team has determined that HRC-S gain correction and PI region filtering has become problematic since since early 2018. Certain assumptions in the previous calibration procedure have fallen through. Hence, and improved time-dependent gain calibration for HRC-S has been developed, resulting in the two new T_GMAP files above. Further details are presented in Section III.b technical details below.

See the HRC-S T_GMAP why page for more general information on the time-dependent gain correction for HRC-S.

The primary advantage of an accurate time-dependent gain map is to allow for optimal background filtering of events in PI space, using a corresponding PI Region Filter (TGPIMASK2 in CalDB). The new T_GMAP calibrations are most accurate from Launch Date through 2021-05-14T00:00:00 (UTC), the effective date of the most recent HRC-S High Voltage adjustment. The LETGS calibration team has recommended that PI region filtering with these new T_GMAPs be done for OBS_IDs taken before that date, but not after that date, until a new T_GMAP is provided for the new HV settings. The CalDB Manager has therefore implemented a Calibration Validity End Date (CVED0001, with CVET0001) of 2021-05-14T00:00:00 in the two PI Region Filter files above.

NOTE for CIAO 4.13 users:The chandra_repro script requires some intervention to accommodate this CalDB change to the PI Region Filters for any LETG/HRC-S OBS_IDs taken after the recent HV setting change on HRC-S. Specifically, either a modified version of chandra_repro (included in CIAO contributed scripts package 4.13.3, released simultaneously with CalDB 4.9.6), or a user-specified parameter setting with an older version of chandra_repro will be necessary, for all OBS_IDs with DATE-OBS later than 2021-05-14T00:00:00 (UTC). Users who do not have the new chandra_repro must use the parameter setting "pi_filter-" (or "pi_filter=no") with the chandra_repro command, to shut off the PI region filtering step, or an error will occur that halts the procedure without building the level 2 events list (*evt2.fits) or the spectrum file (*pha3.fits). The error message (not very explanatory) appears as:

# chandra_repro (04 March 2021): ERROR_out() missing 2 required positional arguments: 'msg' and 'val'

For CIAO 4.12 users, the chandra_repro script must not be used for any LETG/HRC-S observations with CIAO 4.12 and CalDB 4.9.6, because it does not apply the correct PI Region Filter for the new T_GMAPs. Instead, the reprocessing of any LETG/HRC-S OBS_IDs must be done manually in order to implement the new T_GMAPs with the appropriate PI region filter; The PI region filter step must be skipped for OBS_IDs taken after the most recent HRC-S HV change.

PIPELINES/TOOLS AFFECTED:

HRC Level 1 Processing Tool (SDP): hrc_process_events

CIAO reprocessing script: chandra_repro, which uses hrc_process_events.

THREADS AFFECTED:

Reprocessing Data to Create a New Level=2 Event File

C. HRC-S QE N0016 & QEU N0015 File Sets

Location:	$CALDB/data/chandra/hrc/qe/
Filenames:	hrcsD1999-07-22qeN0016.fits hrcsD2012-03-29qeN0016.fits hrcsD2021-05-14qeN0016.fits

Location:

$CALDB/data/chandra/hrc/qeu/

Filenames:

hrcsD1999-07-22qeuN0015.fits hrcsD2000-01-01qeuN0015.fits hrcsD2001-01-01qeuN0015.fits hrcsD2002-01-01qeuN0015.fits hrcsD2003-01-01qeuN0015.fits hrcsD2004-01-01qeuN0015.fits hrcsD2005-01-01qeuN0015.fits hrcsD2006-01-01qeuN0015.fits hrcsD2007-01-01qeuN0015.fits hrcsD2008-01-01qeuN0015.fits hrcsD2009-01-01qeuN0015.fits hrcsD2009-08-08qeuN0015.fits hrcsD2010-09-14qeuN0015.fits hrcsD2012-03-29qeuN0015.fits hrcsD2012-10-05qeuN0015.fits hrcsD2013-09-21qeuN0015.fits hrcsD2015-02-17qeuN0015.fits hrcsD2016-02-22qeuN0015.fits hrcsD2016-07-28qeuN0015.fits hrcsD2017-01-23qeuN0015.fits hrcsD2017-06-05qeuN0015.fits hrcsD2017-09-26qeuN0015.fits hrcsD2018-01-19qeuN0015.fits hrcsD2018-05-27qeuN0015.fits hrcsD2018-09-26qeuN0015.fits hrcsD2019-02-24qeuN0015.fits hrcsD2019-08-22qeuN0015.fits hrcsD2020-01-16qeuN0015.fits hrcsD2020-07-22qeuN0015.fits hrcsD2021-05-14qeuN0015.fits

An full upgrade is being released to the QE/QEU calibration for HRC-S, including the two new time-dependent file sets listed above. The three QE N0016 files are effect at Launch Date, at the 2012-03-29 HV setting adjustment, and the 2021-05-14 HV adjustment dates, respectively. Meanwhile, the secular time variations in the HRC-S response are subsumed now into the numerous QEU maps version N0015.

See the HRC-S QE/QEU why page for information on the current HRC-S QE and QE Uniformity. See the technical details section below for illustrations and details of the derivation of these new QE Uniformity corrections.

SDP Pipeline / CIAO SCRIPTS/TOOLS AFFECTED:

The SDP pipeline procedure "tg_mk_responses" is used to generate single-source GARFs and GRMFs for HRC-S/LETG observations, to be ingested onto the archive. This procedure uses the HRC-S QEU library as loaded from the ARDLIB.

See the CIAO script fluximage, which uses mkinstmap.

THREADS AFFECTED:

For exposure-corrected imaging analysis with HRC-S, see the thread:

• HRC-S Exposure Map and Exposure-corrected Image

For grating spectroscopy with the LETG/HRC-S, see the thread:

• LETG/HRC-S Grating ARFs

D. HRC-I QE N0013 File Set

Location:

$CALDB/data/chandra/hrc/qe/

Filenames:

hrciD1999-07-29qeN0013.fits hrciD2000-07-23qeN0013.fits hrciD2001-04-17qeN0013.fits hrciD2001-10-12qeN0013.fits hrciD2002-04-12qeN0013.fits hrciD2002-10-23qeN0013.fits hrciD2003-04-23qeN0013.fits hrciD2003-10-06qeN0013.fits hrciD2004-04-05qeN0013.fits hrciD2004-11-05qeN0013.fits hrciD2005-05-15qeN0013.fits hrciD2005-11-01qeN0013.fits hrciD2006-04-25qeN0013.fits hrciD2006-11-19qeN0013.fits hrciD2007-09-15qeN0013.fits hrciD2008-09-11qeN0013.fits hrciD2009-09-15qeN0013.fits hrciD2010-09-16qeN0013.fits hrciD2011-09-29qeN0013.fits hrciD2012-09-29qeN0013.fits hrciD2013-10-03qeN0013.fits hrciD2014-09-29qeN0013.fits hrciD2015-08-05qeN0013.fits hrciD2016-06-11qeN0013.fits hrciD2017-02-16qeN0013.fits hrciD2017-08-16qeN0013.fits hrciD2018-02-12qeN0013.fits hrciD2018-08-24qeN0013.fits hrciD2019-02-27qeN0013.fits hrciD2019-08-24qeN0013.fits hrciD2020-02-20qeN0013.fits hrciD2020-08-27qeN0013.fits hrciD2021-01-09qeN0013.fits hrciD2021-02-16qeN0013.fits

The HRC-I Calibration Team has released a modified time-dependent QE file set, which includes the most recent degradations, as determined from calibration source HZ43, and verified using the hard calibration source SNR G21.5-0.9. In addition, a new file has been added coinciding with the recent HRC-I HV adjustment, which is effective as of 2021-02-16T13:09:07, the effective date of the new file. See the technical details section below for specific calibration information.

PIPELINES/TOOLS AFFECTED:

CIAO contributed script: fluximage

THREADS AFFECTED:

CIAO thread: HRC-I Exposure Map and Exposure-corrected Image

E. HRC-S GTI_LIM, T_GMAP Header Mods for Mismatched HV OBS_IDs

Location:	$CALDB/data/chandra/hrc/gti_lim/
Filenames:	hrcsD2002-11-15gtilimN0005.fits hrcsD2012-03-29gtilimN0003.fits

Location:	$CALDB/data/chandra/hrc/t_gmap/
Filenames:	hrcsD1999-07-22t_gmapN0004.fits hrcsD2012-03-29t_gmapN0004.fits

Surrounding the HRC-S 2012-03-29 HV change, certain OBS_IDs were taken with HV settings that were mis-matched from the standard setting for the period during which they were taken. Ten in all have been identified, each of which were given manual processing instructions in the DS Ops OBS_ID reports generated at the time these observations were scheduled. These manual instructions include parameter settings (pset commands) for the HRC-S processing pipelines for the GTI_LIM (mtl_build_gti, standard) and T_GMAP (hrc_process_events). These instructions in some cases specified GTI_LIM files that had not been approved by configuration management. Furthermore, the T_GMAP pset requirement extends to CIAO reprocessing for these ten OBS_IDs, which users might not be aware of when working with these observations.

The Chandra CalDB may be set up in such a way as to alleviate the need for these manual psets, for all future SDP or CIAO reprocessing. Hence, for each of the ten observations in question, the above GTI_LIM and T_GMAP files have had additional CalDB keyword sets added to their FITS headers, to allow automatic selection of the respective files from CalDB without manual intervention.

III. TECHNICAL DETAILS

A. ACIS T_GAIN Epochs 85+86

The general description and method of derivation for the ACIS T_GAIN are given in the memorandum posted on ACIS Calibrationweb page http://cxc.harvard.edu/cal/Acis/Cal_prods/tgain/index.html. However, additional steps have been added to the derivation procedure, due to the ever poorer statistics that are attainable from the ECS due to the source's diminishing flux levels. In particular, the ACIS calibration team has used trends from previous epochs (when more ECS flux was available) to "nudge" their more recent results to provide more predictable time-dependent gain corrections. The method is to combine earlier epochal data with current (i.e. new) epochal data to generate a 12-month average for T_GAIN corrections, and use the trends form the 12-month averages to modify the 6-month averages, resulting in a smoother correction with better statistical support.

The data are increasingly noisy as the ECS flux decreases with the age of the spacecraft. As a result the ACIS team is has selectively increased the range of acceptable operating focal plane temperatures (FP_TEMP values) for all of the 10 chips in order to include more events for better statistics in the T_GAIN correction values. This expanded range is 151.96K to 154.96K.

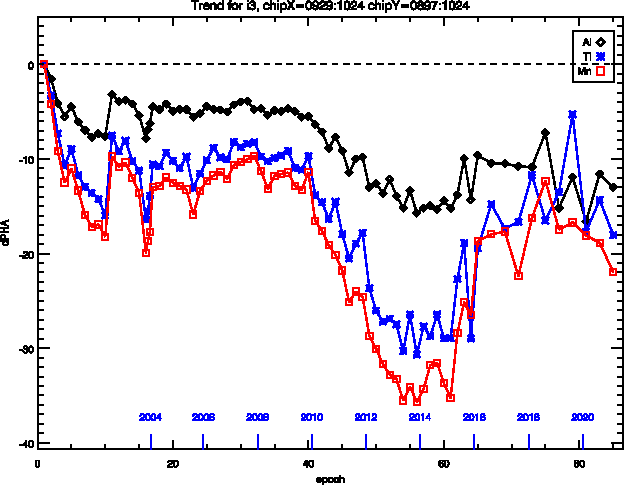
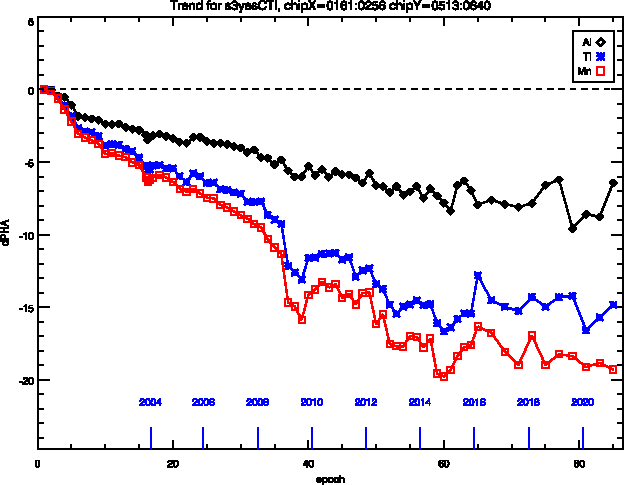
Long term trends for chips I3 and S3 are plotted below in Figures 1a and b, through Epoch 86, which includes the latest release. The chip locations for these plots are given in the respective labels above the plots. The chip locations selected are near the aimpoints. The full CTI corrections have been applied to the data in both figures. While some fluctuations have occurred recently in the results for the Ti and Mn lines of the ECS for I3 in particular, there is nothing out-of-expectation for the newest datasets. The fluctuations in the traces are due to counting statistics.

Fig. 1a: Long-term T_GAIN correction tgain_trends at the ACIS-I3 aimpoint, for specific ECS line energies, from Epoch 1 to Epoch 86.

Fig. 1b: Long term T_GAIN correction tgain_trends at the aimpoint of ACIS-S3, for specific ECS line energies, from Epoch 1 to Epoch 86.

B. HRC-S T_GMAPs N0004; PI Region Filter Cut-off

The following information is adapted from the LETGS calibration web page:

HRC-S Adjustment for Very Low Gain

The calibrations specified therein are included in the new N0004 T_GMAP files proposed for release in CalDB 4.9.6.

Soon after release of the new HRC-S gain calibration (Jun 2020, CALDB 4.9.2) it was discovered that the LETG/HRC-S background filter was sometimes removing more than the intended 1% of valid X-ray events. Excess losses were observed primarily at negative wavelengths for observations beginning c. 2017 and increasing over time (as gain decreased), with losses of up to 6% at some wavelengths by late 2020. Investigation revealed that the shape of event pulse height distributions (PHDs) was becoming subtly distorted at very low gains, with relatively large effects at the high-channel extremes of the PHDs, where the background filter takes effect.

The above web page illustrates the nature of the distortions of the pulse-height distributions which causes more real X-ray events to be mis-identified as background events, and hence to be removed from L2 events and spectra. The corrections alleviate this for 2017-2020 observtions.

Corrections have now been applied to the HRC-S TGAIN (time-dependent gain) coefficients so that the 99th percentile PI values for X-ray events, rather than the medians, are constant (or for certain subtaps, below the filter threshold; see details below). The background filter can now be safely applied for all observations (reprocessed using the T_GMAP N0004 files in CALDB 4.9.6) prior to the HRC-S high voltage change on May 14 2021.

NOTE: The PI Region Filtering should be shut off for OBS_IDs taken AFTER the HV adjustment date 2021-05-14T00:00:00, because new T_GMAP coefficients are needed for those data sets. The new T_GMAP calibrations for this case will not be available for some time. Hence users running the script chandra_repro must use the option pi_filter=no or pi_filter- to avoid applying the PI filtering to their L1.5 event lists before L2 event filtering and PHA2 spectrum extraction.

C. HRC-S QE N0016 & QEU N0015 File Sets

For the QE, the substantial change was the creation of hrcsD2021-05-14qeN0016.fits, whose QE values are 1.106 times those in hrcsD2012-03-29qeN0016.fits. This was the factor needed for observed HRC-S/LETG fluxes to match those expected in zeroth and dispersed orders, for an 18 ksec HZ 43 observation taken after the HV setting update done on May 14 2021.

For the QEU, there is an additional file, hrcsD2021-05-14qeuN0015.fits, effective after the May 14 2021 HV setting update, which updates the outer plates' wavelength dependent corrections, required to match expected HZ 43 flux after taking into account the "grey" linear decline versus time.

Finally, the linear ramps introduced in QE N0014 for wavelengths shorter than 20Å, versus time, have been moved to the QEU N0015. This results in the removal of the annually-varying QE N0014 files, as all the secular variations are being included with the QEU correction files.

D. HRC-I QE N0013 File Set

The new HRC-I QE update are based on HZ 43 observations, and verified with G21.5-0.9. They includes corrections to the most recent QE drop, modeled as a quadratic loss starting from 2016, and a readjustment to the post-HV increase QE assuming that it reset the instrument to c.2018.

Below are plots showing the observed count rate drop and the effect of the correction for HZ 43 (Fig. 2, absolute values in top panel, ratios in bottom panel), and the validation with G21.5-0.9 using the CIAO srcflux tool (Fig. 3, absolute flux not reliable because it adjusts each photon's energy which is not proper for HRC, but relative fluxes are fine).

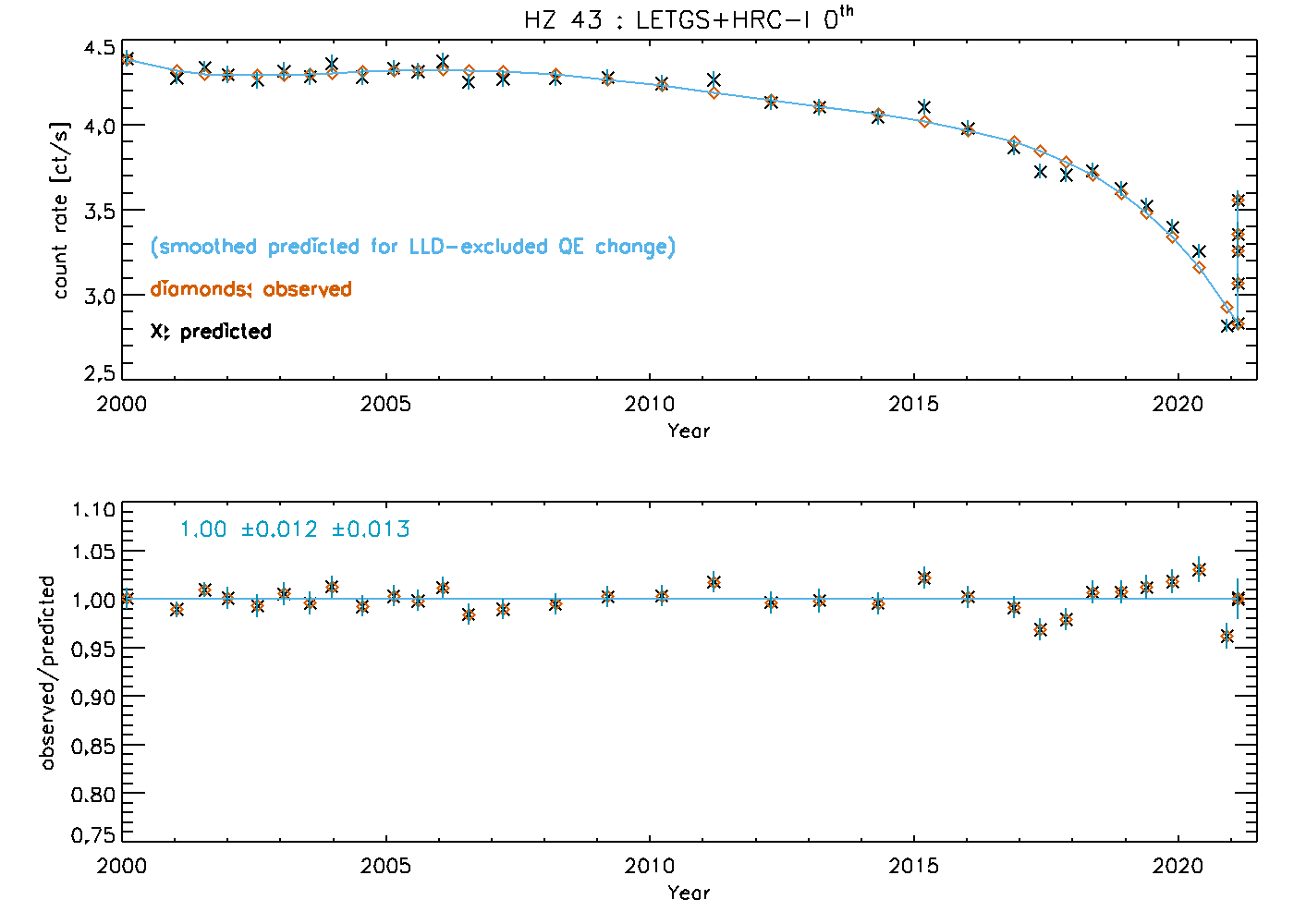
Fig. 2: LETG/HRC-I zeroth-order count rates (top panel: absolute, lower panel: ratios) from HZ43 throughout the mission.
The sharp increase at the end of the curve is from observations during the HV change.

Fig. 3: Relative fluxes from G21.5-0.9 using the CIAO srcflux tool.