|
|
Advice on Minimization Methods
Contents
The Sherpa Optimization
Methods page describes each optimization method in
detail.
The minimization of mathematical functions is a difficult
operation. A general function f(x) of vector argument
x may have many isolated local minima, non-isolated
minimum hypersurfaces, or even more complicated topologies. No
finite minimization routine can guarantee to locate the unique,
global, minimum of f(x) without being fed intimate
knowledge about the function by the user.
This does not mean that minimization is a hopeless task. For
many problems there are techniques which will locate a local
minimum which may be "close enough" to the global minimum, and
there are techniques which will find the global minimum a large
fraction of the time (in a probabilistic sense). However, the
reader should be aware of my philosophy is that there is no
"best" algorithm for finding the minimum of a general
function. Instead, Sherpa provides tools which will allow the
user to look at the overall behavior of the function and find
plausible local minima, will often contain the
physically-meaningful minimum in the types of problem with which
Sherpa deals.
In general, the best assurance that the correct minimum has been
found in a particular calculation is careful examination of the
nature of the solution (e.g., by plotting a fitted function over
data), and some confidence that the full region that the
minimum may lie in has been well searched by the algorithm
used. This document seeks to give the reader some information
about what the different choices of algorithm will mean in terms
of run-time and confidence of locating a good minimum.
Some points to take away from the discussions in the rest of
this document.
-
Never accept the result of a minimization using a single
optimization run; always test the minimum using a different
method.
-
Check that the result of the minimization does not have
parameter values at the edges of the parameter space. If
this happens, then the fit must be disregarded since the
minimum lies outside the space that has been searched, or
the minimization missed the minimum.
-
Get a feel for the range of values of the target function
(in Sherpa, this is the fit statistic), and the stability
of the solution, by starting the minimization from several
different parameter values.
-
Always check that the minimum "looks right" using a plotting
tool.
Sherpa contains two types of routine for minimizing a fit
statistic. I will call them the "single-shot" routines, which
start from a guessed set of parameters, and then try to improve
the parameters in a continuous fashion, and the "scatter-shot"
routines, which try to look at parameters over the entire
permitted hypervolume to see if there are better minima than
near the starting guessed set of parameters.
As the reader might expect, the single-shot routines are
relatively quick, but depend critically on the guessed initial
parameter values x0 being near (in
some sense) to the minimum xmin. All
the single-shot routines investigate the local behaviour of the
function near x0, and then make a
guess at the best direction and distance to move to find a
better minimum. After testing at the new point, they accept that
point as the next guess, x1, if the
fit statistic is smaller than at the first point, and modify the
search procedure if it isn't smaller. The routines continue to
run until either
-
all search directions result in an increased value of the
fit statistic;
-
an excessive number of steps have been taken; or
-
something strange happens to the fit statistic (e.g., it
turns out to be discontinuous in some horrible way).
This description indicates that for the single-shot routines,
there is a considerable emphasis on the initial search position,
x0, being reasonable. It may also be
apparent that the values of these parameters should be moderate;
neither too small (10-12, say), nor too large
(1012, say). This is because the initial choice
of step size in moving from x0 towards
the next improved set of parameters,
x1, is based on the change in the fit
statistic, f(x) as components of x are varied
by amounts
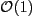 . If
f varies little as x is varied by this amount,
then the calculation of the distance to move to reach the next
root may be inaccurate. On the other hand, if f has a
lot of structure (several maxima and minima) as x is
varied by the initial step size, then these single-shot
minimizers may mistakenly jump entirely over the "interesting"
region of parameter space. . If
f varies little as x is varied by this amount,
then the calculation of the distance to move to reach the next
root may be inaccurate. On the other hand, if f has a
lot of structure (several maxima and minima) as x is
varied by the initial step size, then these single-shot
minimizers may mistakenly jump entirely over the "interesting"
region of parameter space.
These considerations suggest that the user should arrange that
the search vector is scaled so that the range of parameter space
to be searched is neither too large nor too small. To take a
concrete example, it would not be a good idea to have
x7 parameterize
NH in a spectral fit, with an initial
guess of 1020, and a search range
1016 to 1024 (units assumed to
be cm-2). The minimizers will look for
variations in the fit statistic as NH
is varied by 1 cm-2, and finding none (to the
rounding accuracy likely for the code), will conclude that
x7 is close to being a null parameter
and can be ignored in the fitting. It would be much
better to have x7 =
log10 (NH), with a
search range of 16 - 24. Significant variations in the fit
statistic will occur as x7 is varied
by ±1, and the code has a reasonable chance of finding a
useful solution.
Bearing this in mind, the single-shot minimizers in Sherpa are:
-
Powell This method is
described in some detail by Press et al. (1986). It is
basically a censored maximum-gradients technique which,
starting from a first guess, moves towards a minimum by
finding a good direction in which to move, and calculating a
sensible distance to go. Its principal drawback is that to
calculate the distance to move it has to make some
assumptions about how large a step size to take, and hence
there is an implicit assumption that the search space is
reasonably well scaled (to ±10 units in each of the
search directions, say). It is also important that in
finding these gradients, the steps do not miss a lot of
important structure; there should not be too many subsidiary
minima. It is possible for the Powell technique to
become trapped in subsidiary minima, and it is possible for
it to skip entirely over a minimum. However, if the initial
set of parameters is not too far from the true minimum,
Powell will usually do a good job of refining the parameter
estimates. Thus Powell is a good technique for
refining a set of parameters to reach a nearby local or
global minimum, but a bad technique for finding a
global minimum of a complicated search space.
-
Simplex This
technique creates a polyhedral search element around the
initial position, x0, and then
grows or shrinks in particular directions while crawling
around parameter space, to try to place a minimum within the
final search polyhedron. This technique has some hilarious
ways of getting stuck in high-dimension parameter spaces
(where the polyhedron can become a strange shape), but is
very good at finding minima in regions where the fit
statistic has a moderately well-defined topology. Since it
works in a different way than Powell minimization, a good
strategy is to combine Simplex and Powell minimization to
test whether an apparent minimum found by one technique is
stable when searched by the other. I regard Simplex
searching as good in smooth and simple parameter
spaces, particularly when looking at regions where the fit
statistic depends on a parameter in a linear or parabolic
fashion, and bad where surfaces of equal value of
the fit statistic are complicated. In either case, it is
essential that the initial size of the polyhedron (with
sides of length 1 unit) is a smallish fraction of the search
space.
-
Levenberg-Marquardt
This resembles an improved Powell minimization, constructing
good search directions and distances to move based on the
shape of the target function near the initial guessed
minimum, x0, and then
progressively moving towards the dominant local minimum. The
refinement over Powell minimization is that this technique
uses information about the local curvature of the fit
statistic as well as its local gradients, and this tends to
stabilize the result in some cases. I regard the techniques
implemented in Sherpa as being good
minimum-refiners for simple local topologies, since more
assumptions about topology are made than in the Simplex or
Powell methods, but bad at finding global minima
for target functions with complicated topologies.
Although a bit ad hoc, these techniques attempt to
locate a decent minimum over the entire range of the search
parameter space. Because they involve searching a lot of the
parameter space, they involve many function
evaluations, and are somewhere between quite slow and incredibly
tediously slow.
The scatter-shot routines are:
-
Grid This routine
simply searches a grid in each of the search parameters. The
coarseness of the grid sets how precise a root will be
found. If, for example, there are 4 parameters to be
searched (i.e., x is a vector of dimension 4), then
with 131072 grid points (the default), there will be 19
sample points on each axis of the 4-D search space, and so
the accuracy of estimation of each parameter will be roughly
0.06 of the range of the axis in that parameter. If the fit
statistic has significant structure on a smaller scale, then
the grid-searcher will miss it completely. This is a
good technique for finding an approximation to the
minimum for a slowly-varying function. It is a bad
technique for getting accurate estimates of the location of
a minimum, or for examining a fit statistic with lots of
subsidiary maxima and minima within the search space.
-
Monte
Carlo This is even simpler than the
grid-search routine. A certain number of random samples of
the target function are made, with each element of the test
parameter vector, x, sampled uniformly from the
specified search range. Clearly this routine is
probabilistic; even for a smoothly-varying target function,
there is a chance that no sample will lie particularly close
to the minimum. On the other hand, for a function with
unknown properties, this technique does give a chance of
finding a minimum even in some part of parameter space that
might not be thought of in the first place. Again, this is a
good technique for finding rough minima for
slowly-varying functions, and a bad technique for
getting accurate minima, or minima for functions with a lot
of structure in the search space.
-
Monte-Powell
This technique attempts to cope with complicated functions
by looking for minima near a large number of
randomly-selected locations within the designated search
space. It turns out that this is surprisingly good at
finding the global minimum of even quite complicated
functions provided that enough initial start points are
chosen. Difficulties may be encountered if the global
minimum is in a very small part of parameter space (i.e., if
the minimum is very sharp), while there are other,
shallower, minima which occupy a larger fraction of the
parameter space and which are likely to capture the Powell
minimizations. Thus this is a good technique for
many functions, and tends to be bad only for
functions which are genuinely difficult anyway. It is my
personal favorite for exploring a new function about which I
know rather little, because it makes no special assumptions
about the target function, but it is rather inefficient
since many function evaluations are far from the center of
parameter space.
-
Grid-Powell This
is similar to Monte-Powell, except that a regular grid of
points is searched, rather than allowing a probabilistic
sampling of the parameter space. For low-dimension spaces
(i.e. small number of parameters) in which there is rather
little structure this may be good, but for higher-dimension
spaces (i.e. large number of parameters) the sampling of the
grid becomes unacceptably coarse and finding the correct
global minimum can be a considerable fluke (worse even than
in Monte-Powell) because many of the function evaluations
are forced to lie at the edge of the parameter space,
relatively far from the guessed minimum. Thus, for example,
if an 8-D space is to be sampled, there are only 4 samples
on each axis, and if the fit statistic has significant
structure on the scale of a quarter of any one of the search
parameters, it is likely that the global minimum will be
missed. I regard Grid-Powell as a good method for
functions where I know enough about the function that I can
bracket the minimum with some certainty, but a bad
technique for high-dimension minimizations.
-
Simulated Annealing There are
four such methods available in Sherpa. All are statistical
methods for trying to find a global minimum in a complicated
parameter space. The details of the various simulated
annealing techniques are given in SIMUL-ANN-1 and SIMUL-ANN-2. Basically these
methods make considerable improvements on the Monte Carlo
technique, by spending fewer function evaluations in
unproductive bits of parameter space (where the target
function is far from the minimum), and more function
evaluations near the minimum. The way this is done borrows
some techniques from statistical mechanics, but the
essential detail is that this is a conditioned
probabilistic approach to finding the minimum. It tends
to be good at finding an answer which is fairly
close to the global minimum, but it is bad in that
all four the simulated annealing methods use tremendous
amounts of CPU time. These techniques are a high order of
overkill in relatively simple minimization problems, but for
truly difficult problems where the user has little or no
idea what the real answer is, they provide a brute-force way
of getting an answer which is fairly reliable. The
techniques that combine Powell minimization with simulated
annealing tend to be better than the pure simulated
annealing methods; they produce better estimates of the
minima.
Overall, the single-shot methods are best regarded as ways of
refining minima located in other ways: from good starting
guesses, or from the scatter-shot techniques. Using intelligence
to come up with a good first-guess solution is the best
approach, when the single-shot refiners can be used to get
accurate values for the parameters at the minimum. However, I
would certainly recommend running at least a second single-shot
minimizer after the first, to get some indication that one set
of assumptions about the shape of the minimum is not
compromising the solution. It is probably best if the code
rescales the parameter range between minimizations, so that a
completely different sampling of the function near the trial
minimum is being made.
Since they tend to be slow, repeated rescaled runs are rarely
possible with the scatter-shot minimizers. For most relatively
well-behaved functions where quality control over the estimated
parameters is being made by an intelligent user, I would
recommend running Monte-Powell or Grid-Powell and then testing
the minimum using the Simplex or Levenberg-Marquardt
routines. If an automatic minimum-finder is being written, then
I would run the scatter-shot minimizer at least twice, with the
second run using a restricted range of search space around the
minimum from the first, and then test the minimum using
single-shot minimizers. For functions where little is known
about their properties, or for problems where the user has an
almost unlimited CPU time available to reach the "right" answer,
I would use one of the simulated annealing plus Powell
minimizers, follow up with a Grid-Powell minimizer, and then
finish off with a Simplex or Levenberg-Marquardt minimizer. Even
then, I wouldn't believe the solution until I'd looked at it
pretty carefully: there are plenty of rogue functions out there!
| Class of Technique |
Type |
Speed |
Commentary |
| Powell |
single-shot |
fast |
OK for refining minima |
| Simplex |
single-shot |
fast |
OK for refining minima |
| Levenberg-Marquardt |
single-shot |
fast |
OK for refining minima |
| Grid |
scatter-shot |
slowish |
OK for smooth functions, grid-quantized minima, quad may
need fine grid. |
| Monte Carlo |
scatter-shot |
slowish |
OK for smooth functions, quad only gives rough minima, quad
usually needs many random start points. |
| Monte-Powell |
scatter-shot |
slowish |
OK for many functions, quad usually needs many random start
points. |
| Grid-Powell |
scatter-shot |
slowish |
OK for smooth functions, quad may need fine grid. |
| Simulated annealing |
scatter-shot |
very slow |
Good in many cases, quad use if desperate measures are
needed. |
The contents of this document are taken from a memo written by
Mark Birkinshaw (1998).
|




