Next: 6. Sherpa Fit Statistics Up: Sherpa Reference Manual Previous: 4. Sherpa Optimization Methods
The primary task of Sherpa is to fit a model
![]() to a set of observed data.
to a set of observed data. ![]() denotes
the set of model arguments,
denotes
the set of model arguments, ![]() denotes the model
parameters, and
denotes the model
parameters, and ![]() denotes model options.
denotes model options.
The modeling aspect of Sherpa is designed with complete generality in mind. Sherpa provides the user with a set of commonly used 1- and 2-D models, some of which are unique to Sherpa , and some of which come directly from Version 11 of XSPEC (Arnaud 1996). The user is free to combine these models to build arbitrarily complex composite models.5.1The user can also rename models, and apply them along any data axis. Thus the user can provide three names for the 1-D power-law model POWLAW1D and build a 3-D composite power-law model with different photon indices along each axis. (The photon index values could also be linked between different axes.) Finally, Sherpa also provides the user with the capability of inputting his or her own model (see USERMODEL below).
There are three model categories in Sherpa : source, background, and instrument. Each is discussed in turn below. Models from different categories can be combined during the fitting process. The user can combine background and source models when fitting background-subtracted data, or convolve source and instrument models when fitting PSF-broadened spatial data. Sherpa does not require the user to specify models in all three categories; only the source model is required.
Sherpa uses the concept of `source models' in order to highlight their specific physical meaning. They describe parent distributions from which the observed source data may have been sampled. While many of the Sherpa source models have physical interpretation, many are phenomenological, serving only as a mathematical parameterization of the observed data.
Source models may be compared to the observed data in two different ways:
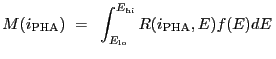 |
(5.1) |
Sherpa provides a number of 1-D source models that the user may apply to any kind of 1-D data, or may combine together to create arbitrarily complex source models. For instance, one could use POWLAW1D to model energy spectra, SIN to model a binned time series (e.g. a light curve), and GAUSS to arbitrary non-astrophysical data provided in an ASCII file.
Sherpa also provides a number of 2-D source models that the user may apply to any kind of 2-D data, or may combine together to create arbitrarily complex source models. For instance, one could use BETA2D or GAUSS2D to fit image data. These 2-D models are sometimes referred to as spatial models in this manual, since it is envisioned that their use will be primarily to fit 2-D image data.
Chandra is capable of making simultaneous high resolution measurements of a photon's spatial location, energy, and time-of-arrival. Thus the user may wish to combine 1-D and/or 2-D models to create arbitrarily complex 2-D, 3-D, or 4-D models to fit these data. Examples of analyses which require such multi-dimensional models include:
As stated above, Sherpa allows the user to combine 1-D models so as to model a 2-D dataset (with, say, energy and time axes). Note however that in the current version of Sherpa it is not yet possible to combine 1-D and/or 2-D instrument models, i.e. the user cannot yet convolve an arbitrary multi-dimensional model with a multi-dimensional instrument model. Such functionality will be provided in a future version of the software.
In the analysis of binned data, source model functions can be split into two classes. The first class contains the ``additive" models, which are integrated over bins in energy-space (before being folded through an instrument), or over bins in counts-space (if no instrument model is specified). The second class contains the ``multiplicative" models, which are not integrated when evaluated. Additive models can describe photon generation (e.g. BBODY), while multiplicative models can describe photon attenuation (e.g. ATTEN) or filtering (e.g. BOX1D). Note that in Sherpa , multiplicative model amplitudes for binned data are currently evaluated at the lower boundary of each bin.
In Sherpa , some models are integrated by default, including all
XSPEC additive models
(see Table 5.9 and the XSPEC Version 11
User's Guide).
Sherpa lets the user control the integration of non-XSPEC source models
(i.e. those models unique to Sherpa ) when fitting binned data, by using the
INTEGRATE ![]() ON|OFF
ON|OFF![]() command.
An example of a
situation in which the user may wish
to change the integration status of a source model is when it is used
in nested model expressions.
command.
An example of a
situation in which the user may wish
to change the integration status of a source model is when it is used
in nested model expressions.
Background models are in every way like source models, except that they are used to describe parent distributions from which observed background data may have been sampled. These data are input using the BACK command. Depending on the type of statistical analysis, these data can be subtracted from the observed raw counts data or can be simultaneously modeled with the source data. Background models are specified using the BACKGROUND | BG command. note that any model component in the Sherpa library may be used to compose a background model.
Instrument models describe instrument characteristics, such as an effective area, a detector's energy response, or a mirror's point-spread function. They are convolved with the source, background, or combined source and background model to compute the number of predicted counts in each detector bin.
Instrument models may also be defined with analytic functions. The current version of Sherpa allows the user to define instrument models using functions defined in the TCD library (the Transformation, Convolution and Deconvolution tools). These include 1-D and 2-D Gaussian, box, and top-hat functions. The relevant command is TPSF.
The INSTRUMENT command has more details on modeling the instrument in source or background data analysis.
The following instrument models are available in Sherpa 3.2:
| Model | Description |
|---|---|
| FARF1D | FARF | A 1-D file-based ancillary response model |
| FARF2D | FEXPMAP | FEXPMAP2D | A 2-D file-based ancillary response model |
| FPSF1D | A 1-D file-based PSF instrument model |
| FPSF2D | FPSF | PSFFROMFILE | A 2-D file-based PSF instrument model |
| FRMF1D | FRMF | A 1-D file-based response matrix model |
| KERNEL | A 1-D convolution model. |
| PTSRC1D | A 1-D file-based point-source fitting model |
| PTSRC2D | PTSRC | A 2-D file-based point-source fitting model |
| RSP1D | RSP | A 1-D instrument model. |
| RSP2D | A 2-D instrument model. |
| TPSF1D | A 1-D TCD-model-based PSF instrument model |
| TPSF2D | TPSF |PSFFROMTCD | PSF | A 2-D TCD-model-based PSF instrument model |
More information on each model is available at the end of this chapter.
The following syntax establishes a model component for usage in the current Sherpa session:
sherpa> ![]() CREATE
CREATE![]()
![]() sherpa_modelname
sherpa_modelname![]()
(The brackets around CREATE indicate that its use is optional; see examples below.) In addition, Sherpa provides the user with the ability to both establish a model component, and to assign to it an arbitrary name:
sherpa> ![]() CREATE
CREATE![]()
![]() sherpa_modelname
sherpa_modelname![]() [
[![]() modelname
modelname![]() ]
]
where ![]() sherpa_modelname
sherpa_modelname![]() is the
Sherpa default
model name (or an XSPEC model name,
with the prefix `xs' attached), and
is the
Sherpa default
model name (or an XSPEC model name,
with the prefix `xs' attached), and ![]() modelname
modelname![]() is the name being
given to the model component by the user. Note that
is the name being
given to the model component by the user. Note that ![]() modelname
modelname![]() must be enclosed in brackets,
must be enclosed in brackets, ![]()
![]() .
.
Sherpa 's ability to assign arbitrary names to model components allows the user to establish multiple independent models of the same type during a single session, and is a valuable feature of the software. (See Example 7.) Note that an assigned model name can be any arbitrary string, except a string that is already a Sherpa command.
By default, Sherpa will prompt the user for the initial model component parameter values.5.3At the model parameter prompt, the user may either:
| Argument: | Description: |
|---|---|
| Model parameter initial value. | |
| Minimum value for that parameter range. | |
| Maximum value for that parameter range. | |
| Specifies initial parameter step size. | |
| ,-1 | Sets the parameter to be frozen. |
Note that the default setting for delta is 1% of the parameter value. Otherwise, specifying delta will set the initial parameter step size to an absolute value. The parameter step size is used by the optimization method to determine where to sample parameter space. As such, if the value of a parameter is known well, then specifying a small delta may lead to a substantially faster and better fit.
Note that this colon separated list need not include all of the elements, but it does need to maintain the proper sequential order, and also include the colons around skipped elements (up to three elements only). Also, there cannot be a space between the , and the -1.
The model components that have been established in the current Sherpa session, and their parameter information, may be listed with the command SHOW MODELS. Note however that information about model parameter delta settings is currently not returned by SHOW. Information about model parameter delta settings is included when using SAVE.
sherpa> CREATE POLY POLY.c0 parameter value [1] POLY.c1 parameter value [0] POLY.c2 parameter value [0] POLY.c3 parameter value [0] POLY.c4 parameter value [0] POLY.c5 parameter value [0] POLY.c6 parameter value [0] POLY.c7 parameter value [0] POLY.c8 parameter value [0] POLY.offset parameter value [0]The command CREATE POLY establishes the Sherpa model POLYNOM1D as a model component available for usage in the current Sherpa session. Note that after issuing this command, the user is prompted for the initial model parameter values. In this example, the user accepted the given initial values for all of the parameters, using the
sherpa> POLY
sherpa> CREATE POLY[modela] modela.c0 parameter value [1] modela.c1 parameter value [0] modela.c2 parameter value [0] modela.c3 parameter value [0] modela.c4 parameter value [0] modela.c5 parameter value [0] modela.c6 parameter value [0] modela.c7 parameter value [0] modela.c8 parameter value [0] modela.offset parameter value [0]The command CREATE POLY
sherpa> POLY[modela]
sherpa> GAUSS[modelb] modelb.fwhm parameter value [10] 2.0:1:10:0.5 modelb.pos parameter value [0] 1:0.1: modelb.ampl parameter value [1] 3::100:2,-1This example establishes and assigns the name modelb to the Sherpa model component GAUSS1D. Note that in this example the user entered an initial value of 2.0, a minimum range value of 1, a maximum range value of 10, and an initial parameter step size delta of 0.5 for parameter fwhm; entered a value of 1, and a minimum range value of 0.1 for parameter pos; and entered a value of 3, a maximum range value of 100, and an initial parameter step size of 2 for parameter ampl, and froze this parameter.
sherpa> GAUSS[modelbb] modelbb.fwhm parameter value [10] 2.0:1:10 modelbb.pos parameter value [0] 1:0.1: modelbb.ampl parameter value [1] 3::100,-1This example establishes and assigns the name modelbb to the Sherpa model component GAUSS1D. Note that in this example the user entered an initial value of 2.0, a minimum range value of 1, and a maximum range value of 10 for parameter fwhm; entered a value of 1, and a minimum range value of 0.1 for parameter pos; and entered a value of 3, and a maximum range value of 100 for parameter ampl, and froze this parameter (note that after the maximum range value, specification of initial parameter step size delta is optional and may be omitted).
sherpa> XSBBODY[modeld] modeld.kT parameter value [3] modeld.norm parameter value [1] ,-1This command establishes and assigns the name modeld to the XSPEC model component bbody. In this example, the user accepted the given initial values for all of the parameters, using the
sherpa> PARAMPROMPT OFF Model parameter prompting is off sherpa> POW[modelc]The first command turns off prompting for model parameter values. The second command establishes the Sherpa model component POWLAW1D, and assigns to it the name modelc. Since parameter prompting was turned off, the model is automatically established using the given initial values for all of the parameters.
sherpa> ERASE ALL sherpa> PARAMPROMPT ON Model parameter prompting is on sherpa> POW[modelc] modelc.gamma parameter value [0] 1.0 modelc.ref parameter value [1] modelc.ampl parameter value [1] sherpa> POW[modelc2] modelc2.gamma parameter value [0] 2.0 modelc2.ref parameter value [1] modelc2.ampl parameter value [1]The third command establishes the Sherpa model component POWLAW1D, and assigns to it the name modelc. In this example, the user set parameter gamma of model component modelc to the value of 1.0. The last command establishes another Sherpa model component POWLAW1D, and assigns to it the name modelc2. In this example, the user set parameter gamma of model component modelc2 to the value of 2.0. Note that model components modelc and modelc2 are independent of one another:
sherpa> SHOW MODELS
Current Composite Models are:
Current Model Components are:
powlaw1d[modelc]
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 gamma thawed 1 -10 10
2 ref frozen 1-3.4028e+38 3.4028e+38
3 ampl thawed 1 0.0000 3.4028e+38
powlaw1d[modelc2]
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 gamma thawed 2 -10 10
2 ref frozen 1-3.4028e+38 3.4028e+38
3 ampl thawed 1 0.0000 3.4028e+38
It is important to note that when a model component is established, if a dataset has been input, then estimates based on the (filtered) data are automatically made for the initial parameter values and their minimum and maximum ranges. However, if no dataset has been input, then the initial parameter values and ranges are assigned arbitrary default values.
If multiple datasets have been input, and if no dataset is indicated in the model expression, then automatic parameter estimates are based on the lowest numbered dataset; for instance, if the user inputs
sherpa> DATA 1 example1.dat sherpa> DATA 2 example2.dat sherpa> POLY[modela]
then the estimates of modela's parameter values are based on the first dataset. Otherwise, if multiple datasets have been input, and a dataset is indicated in the model expression, then the automatic parameter estimates are made based on the indicated dataset; for instance, if the user inputs
sherpa> DATA 1 example1.dat sherpa> DATA 2 example2.dat sherpa> SOURCE 2 = POLY[modela]
then the estimates of modela's parameter values are based on the second dataset.
The user may always obtain updated estimates using the command GUESS (see Example 3 of Section 1.43). Updated estimates may be needed if:
The user may of course wish to directly set initial parameter values and ranges; see Sections 5.4.1, 5.4.3, 5.4.4, and 5.4.5.
sherpa> ERASE ALL
sherpa> POW[modelc]
modelc.gamma parameter value [0]
modelc.ref parameter value [1]
modelc.ampl parameter value [1]
sherpa> SHOW modelc
powlaw1d[modelc]
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 gamma thawed 0 -10 10
2 ref frozen 1-3.4028e+38 3.4028e+38
3 ampl thawed 1 0.0000 3.4028e+38
Here, a model component is established prior to input of data,
so the given initial model parameter values are
pre-set arbitrary defaults. In this example, the user accepts
these values using the
sherpa> ERASE ALL
sherpa> DATA example.pha
sherpa> POW[modelc]
modelc.gamma parameter value [0]
modelc.ref parameter value [1]
modelc.ampl parameter value [0.0010453]
sherpa> SHOW modelc
powlaw1d[modelc]
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 gamma thawed 0 -10 10
2 ref frozen 1 0 94
3 ampl thawed 0.0010 0.0000 0.0021
In this example, the ERASE ALL command is used
to remove the previous model setup. Next, data
are input, with the command DATA example.pha.
This is then followed by the establishment of
the model component, with the command POW[modelc].
Notice that the given initial model parameter values
and ranges are estimates based on the filtered data.
Compare this example to example 1.
sherpa> ERASE ALL
sherpa> POW[modelc]
modelc.gamma parameter value [0]
modelc.ref parameter value [1]
modelc.ampl parameter value [1]
sherpa> DATA example.pha
sherpa> SHOW modelc
powlaw1d[modelc]
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 gamma thawed 0 -10 10
2 ref frozen 1-3.4028e+38 3.4028e+38
3 ampl thawed 1 0.0000 3.4028e+38
sherpa> GUESS modelc
sherpa> SHOW modelc
powlaw1d[modelc]
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 gamma thawed 0 -10 10
2 ref frozen 1 0 94
3 ampl thawed 0.0010 0.0000 0.0021
In this example, the ERASE ALL command is used
to remove the previous input data and model component setups.
Next, a model component is established prior to input of data
(with the command POW[modelc]), and
so the given initial parameter values are default values. The
GUESS command is then used to obtain
parameter value and range estimates, based on the input
dataset.
The model components that have been established in the current Sherpa session, and their parameter information, may be listed with the command SHOW MODELS. Values for these established model component parameters may be set individually using one of the following command syntax options:
sherpa> ![]() CREATE
CREATE![]()
![]() modelname
modelname![]() .{
.{![]() paramname
paramname![]() |
| ![]() #
#![]() } {=
} {= ![]() value
value![]() | =
| =![]()
![]() paramExpr
paramExpr![]() }
}
sherpa> ![]() CREATE
CREATE![]()
![]() modelname
modelname![]() .{
.{![]() paramname
paramname![]() |
| ![]() #
#![]() }.VALUE =
}.VALUE = ![]() value
value![]()
where:
| Argument: | Description: |
|---|---|
| A name given to a model component by the user. | |
| { |
Specifies the parameter whose value is to be set. |
| A number value to which the parameter should be set. | |
| = |
A syntax for linking parameters. |
Note that either ![]() paramname
paramname![]() or
or ![]() #
#![]() may specify the parameter whose value is to be set.
may specify the parameter whose value is to be set.
Note also that parameter values may be set interactively from a plot: Please see command GETX for information on interactively assigning an x-axis value to a model parameter, from a plot; see command GETY for information on interactively assigning a y-axis value.
In addition, the minimum, maximum, and initial delta for parameters may also be individually set, using one of the following applicable command syntax options:
sherpa> ![]() CREATE
CREATE![]()
![]() modelname
modelname![]() .{
.{![]() paramname
paramname![]() |
| ![]() #
#![]() }.MIN =
}.MIN = ![]() value
value![]()
sherpa> ![]() CREATE
CREATE![]()
![]() modelname
modelname![]() .{
.{![]() paramname
paramname![]() |
| ![]() #
#![]() }.MAX =
}.MAX = ![]() value
value![]()
sherpa> ![]() CREATE
CREATE![]()
![]() modelname
modelname![]() .{
.{![]() paramname
paramname![]() |
| ![]() #
#![]() }.DELTA =
}.DELTA = ![]() value
value![]()
sherpa> ERASE ALL sherpa> PARAMPROMPT OFF Model parameter prompting is off sherpa> POLY[modela] sherpa> modela.c0 = 3.0The command (modela.c0 = 3.0) gives the value of 3.0 to parameter c0, of modela. Note that modela is the name given by the user to the Sherpa model component POLYNOM1D. The following commands are each equivalent to the final command:
sherpa> modela.c0.VALUE = 3.0 sherpa> modela.1 = 3.0 sherpa> modela.1.VALUE = 3.0
sherpa> POW[modelc] sherpa> modelc.3 = 10.0 sherpa> modelc.3.MIN = 1.0 sherpa> modelc.3.MAX = 100.0The second command, modelc.3 = 10.0, gives the value of 10.0 to parameter number 3, of modelc. The third and fourth commands set the minimum and maximum values for parameter number 3 of this model component.
sherpa> modelc.3.DELTA = 0.05This command sets the parameter's initial step size, delta, to a value of 0.05.
sherpa> ERASE ALL sherpa> POLY[modela] sherpa> GAUSS[modelb] sherpa> modelb.ampl => 0.5*modela.c0The last command in this series uses a model parameter expression, to link the ampl parameter of modelb to 0.5 multiplied by the c0 parameter of modela.
Alternatively, model parameters and ranges may all be set at one time, using a single command:
sherpa> ![]() CREATE
CREATE![]()
![]() modelname
modelname![]() .{
.{![]() paramname
paramname![]() |
| ![]() #
#![]() } =
} = ![]() param
param![]()
where again ![]() modelname
modelname![]() is the name that has been given
to a model component by the user. Note that either
is the name that has been given
to a model component by the user. Note that either ![]() paramname
paramname![]() or
or ![]() #
#![]() may specify the parameter whose value is to be set. The command argument
may specify the parameter whose value is to be set. The command argument
![]() param
param![]() contains the parameter assignments
contains the parameter assignments
![]() value
value![]() :
:![]() min
min![]() :
:![]() max
max![]() :
:![]() delta
delta![]() , where:
, where:
| Argument: | Description: |
|---|---|
| The value for the model parameter. | |
| The minimum for that parameter range. | |
| The maximum for that parameter range. | |
| Specifies initial parameter step size. |
sherpa> POW[modelc] sherpa> modelc.3 = 10.0:1.0:100.0The command modelc.3 = 10.0:1.0:100.0, gives the value of 10.0 to parameter number 3, sets the minimum to 1.0 for this parameter, and sets the maximum to 100.0 for this parameter, of modelc (where modelc is the name given by the user to the Sherpa model component POWLAW1D, with the second command). The following command is equivalent to the third command:
sherpa> modelc.ampl = 10.0:1.0:100.0Compare the syntax of this example to Section 5.4.3, Example 2.
sherpa> modelc.3 = 10.0:1.0:100.0:0.05This command gives the value of 10.0 to modelc parameter number 3, sets the minimum to 1.0 for this parameter, sets the maximum to 100.0 for this parameter, and sets the parameter's initial step size, delta, to a value of 0.05. Compare the syntax of this example to Section 5.4.3, Example 3.
To be especially efficient, one may establish and assign a name to a model component, as well as set model parameters and their ranges, all at one time using a single command:
sherpa> ![]() CREATE
CREATE![]()
![]() sherpa_modelname
sherpa_modelname![]() [
[![]() modelname
modelname![]() ](
](![]() param
param![]()
![]() ,
,![]() param
param![]() ,
,![]() param
param![]() , ...
, ...![]() )
)
where again ![]() sherpa_modelname
sherpa_modelname![]() is the Sherpa default
model name and
is the Sherpa default
model name and ![]() modelname
modelname![]() is the name being
given to the model component by the user. Note that
is the name being
given to the model component by the user. Note that ![]() modelname
modelname![]() must be enclosed in brackets,
must be enclosed in brackets, ![]()
![]() .
The sequential order of
the comma-separated
.
The sequential order of
the comma-separated ![]() param
param![]() arguments indicates
to which model parameter the values will be applied.
That is, the first
arguments indicates
to which model parameter the values will be applied.
That is, the first ![]() param
param![]() argument will apply to
the model's first parameter, the second
argument will apply to
the model's first parameter, the second ![]() param
param![]() to
the model's second parameter, etc.
to
the model's second parameter, etc.
As in the above Subsection, the command argument
![]() param
param![]() contains the parameter assignments
contains the parameter assignments
![]() value
value![]() :
:![]() min
min![]() :
:![]() max
max![]() :
:![]() delta
delta![]() , where:
, where:
| Argument: | Description: |
|---|---|
| The value for the model parameter. | |
| The minimum for that parameter range. | |
| The maximum for that parameter range. | |
| Specifies initial parameter step size. |
The colon separated list for ![]() param
param![]() need not include all of the
elements, but it does need to maintain the proper sequential
parameter order.
need not include all of the
elements, but it does need to maintain the proper sequential
parameter order.
sherpa> ERASE ALL sherpa> POLY[modela](3.0:1.0:4.0)Assigns the name modela to the Sherpa model component POLYNOM1D. Also gives the value of 3.0 to the model's first parameter (in this case parameter c0), sets the minimum to 1.0 for this parameter, and sets the maximum to 4.0 for this parameter.
sherpa> POW[modelc](1, 5, 10)Assigns the name modelc to the Sherpa model component POWLAW1D. Also gives the value of 1.0 to the model's first parameter (in this case parameter gamma), gives the value of 5.0 to the model's second parameter (ref), and gives the value of 10.0 to the model's third parameter (ampl).
sherpa> POW[modelc2](,,10.0:1.0:100.0:0.05)Assigns the name modelc2 to the Sherpa model component POWLAW1D. Also gives the value of 10.0 to the model's third parameter (in this case parameter ampl), sets the minimum to 1.0 for this parameter, sets the maximum to 100.0 for this parameter, and set the initial step size to 0.05 for this parameter.
Model component names may be assigned, model parameters and ranges may be set, and a source or background model may be defined, using a single command:
sherpa> {SOURCE | BACKGROUND} ![]() #
#![]() =
= ![]() sherpa_modelname
sherpa_modelname![]() [
[![]() modelname
modelname![]() ](
](![]() param
param![]()
![]() ,
,![]() param
param![]() ,
,![]() param
param![]() , ...
, ...![]() )
)
where again ![]() sherpa_modelname
sherpa_modelname![]() is the Sherpa default
model name and
is the Sherpa default
model name and ![]() modelname
modelname![]() is the name being
given to the model component by the user. Note that
is the name being
given to the model component by the user. Note that ![]() modelname
modelname![]() must be enclosed in brackets,
must be enclosed in brackets, ![]()
![]() .
The sequential order of
the comma-separated
.
The sequential order of
the comma-separated ![]() param
param![]() arguments indicates
to which model parameter the values will be applied.
That is, the first
arguments indicates
to which model parameter the values will be applied.
That is, the first ![]() param
param![]() argument will apply to
the model's first parameter, the second
argument will apply to
the model's first parameter, the second ![]() param
param![]() to
the model's second parameter, etc.
to
the model's second parameter, etc.
The command argument ![]() param
param![]() contains the parameter assignments
contains the parameter assignments
![]() value
value![]() :
:![]() min
min![]() :
:![]() max
max![]() :
:![]() delta
delta![]() , where:
, where:
| Argument: | Description: |
|---|---|
| The value for the model parameter. | |
| The minimum for that parameter range. | |
| The maximum for that parameter range. | |
| Specifies initial parameter step size. |
The colon separated list for ![]() param
param![]() need not include all of the
elements, but it does need to maintain the proper sequential
parameter order.
need not include all of the
elements, but it does need to maintain the proper sequential
parameter order.
Please also see the SOURCE command and the BACKGROUND command for more information and examples.
sherpa> ERASE ALL sherpa> SOURCE = POLY[modela](3.0:1.0:4.0)With this single command, the name modela is assigned to the Sherpa model component POLYNOM1D, the value of 3.0 is given to the model's first parameter (in this case parameter c0), the minimum of 1.0 is set for this parameter, the maximum of 4.0 is set for this parameter, and then this model is defined as the source model to be used for fitting dataset number 1.
sherpa> SOURCE 2 = GAUSS[modelb](3:2.5:4.403, 1:-10:10, 1:-3.5:3.5) + POW[modelc]With this single command, the following is performed: the name modelb is assigned to the Sherpa model component GAUSS1D; various parameter values and ranges are set for the parameters of modelb; the name modelc is assigned to the Sherpa model component POWLAW1D; a model expression, which is the sum of these two models, is defined as the source model to be used for fitting dataset number 2.
Model components can be used to create model expressions, in conjunction with the SOURCE and BACKGROUND commands (which then are used to fit the data), or with model stacks:
sherpa> {SOURCE | BACKGROUND | ![]() model_stackname
model_stackname![]() } =
} = ![]() modelExpr
modelExpr![]()
Where the model expression, ![]() modelExpr
modelExpr![]() ,
may be composed of one, or more (combined algebraicly),
of the following elements:
,
may be composed of one, or more (combined algebraicly),
of the following elements:
| Model Expression Element: | Description: |
|---|---|
| A Sherpa default model name. | |
| A name that is being given to a Sherpa model component
( |
|
| A name that has been given to a Sherpa model component. | |
| A nested model. | |
| A joint-mode model. |
A model expression may
be an algebraic combination of these elements that may include numerical values and the following
operators: + - * / ( ) ![]()
![]() {}.
{}.
Note that by default, if a model expression includes a model component that has not previously been established, Sherpa will prompt the user for the initial model parameter values for that model component. Parameter prompting can be turned off using the PARAMPROMPT OFF command.
sherpa> PARAMPROMPT OFF Model parameter prompting is off sherpa> POLY[modela] sherpa> SOURCE 1 = modelaThe last command in this series assigns a model expression to the source model for dataset number 1. This model expression contains one model component, modela (which is an arbitrary name that the user has given to the Sherpa model component POLYNOM1D).
sherpa> ATTEN[modelm] sherpa> BBODY[modelh] sherpa> SOURCE 1 = modelm * modelhThis example establishes two model components, modelm and modelh (which are arbitrary names that the user has given to the Sherpa model components ATTEN and BBODY, respectively). The last command assigns the model expression modelm * modelh to the source model for dataset number 1. The following commands each assign various other model expressions to source models for other datasets:
sherpa> SOURCE 2 = 10*(modelm + modelh) sherpa> SOURCE 3 = (modelm - modelh)/2 sherpa> SOURCE 4 = 0.5*modelm + 0.7*modelh
sherpa> ERASE ALL sherpa> SOURCE 1 = ATTEN[modelm] * BBODY[modelh]In this example the user assigns the model expression ATTEN[modelm] * BBODY[modelh] to the source model for dataset number 1. Note that this single command is equivalent to the first series of commands in Example 2, above.
sherpa> ERASE ALL sherpa> PARAMPROMPT ON Model parameter prompting is on sherpa> BACKGROUND = (POW[modelc])/2 modelc.gamma parameter value [0] modelc.ref parameter value [1] modelc.ampl parameter value [1]This command assigns the model expression (POW[modelc])/2, to the background model for dataset number 1. In this example, via parameter prompting, the user accepted the given initial values for all of the parameters, using the
sherpa> PARAMPROMPT OFF
Model parameter prompting is off
sherpa> shape = GAUSS
sherpa> SIN[modeli]
sherpa> COS[modelj]
sherpa> SRC = modeli{shape} + modelj
The second command, shape = GAUSS, creates a
model stack.
The commands SIN[modeli] and COS[modelj]
establish and assign names to the Sherpa model components
SIN and
COS, respectively.
The final command assigns the model expression modeli{shape} + modelj,
to the source model for dataset number 1. In this example, the
model expression is an algebraic combination of a
nested model,
modeli{shape}, and a model component, modelj.
Note that modeli will be evaluated on the output of
the model expression shape (i.e.:
SRC = SIN(GAUSS(x)) + COS(x)).
sherpa> DATA example_img.fits FITSIMAGE
sherpa> POLY[modelaForAxis1]
sherpa> GAUSS[modelbForAxis2]
sherpa> SRC = modelaForAxis1{x1}*modelbForAxis2{x2}
The command POLY[modelaForAxis1] assigns the name modelaForAxis1
to the Sherpa model component POLYNOM1D; likewise
the command GAUSS[modelbForAxis2] assigns the name modelbForAxis2
to the Sherpa model component GAUSS1D.
The final command assigns the model expression modelaForAxis1{x1}*modelbForAxis2{x2},
to the source model for dataset number 1.
This model expression is an algebraic combination of
joint-mode models.
A model stack assigns an arbitrary name to a model expression, for subsequent use in parameter expressions and/or nested models.
sherpa> ![]() model_stackname
model_stackname![]() =
= ![]() modelExpr
modelExpr![]()
where ![]() model_stackname
model_stackname![]() is the name being assigned to the model expression.
is the name being assigned to the model expression.
See Section 5.4.7 Example 5, Section 5.4.9, and Section 5.4.12 Example 3 for further examples.
sherpa> ERASE ALL sherpa> GAUSS[modelb] sherpa> SRC = modelb sherpa> PositionVariation = POLY sherpa> modelb.pos => PositionVariationThe command GAUSS[modelb], assigns the name modelb to the Sherpa model component GAUSS1D. The next command defines this model component as the source model to be used for fitting. The third command, PositionVariation = POLY, assigns a model stack name to the Sherpa default model POLYNOM1D. The final command creates a parameter expression that links the parameter pos of modelb to the model component POLY (via the model stack name PositionVariation). Note that the creation of a model stack is necessary since the following syntax is currently not allowed:
sherpa> ERASE ALL sherpa> SRC = GAUSS[modelb] sherpa> PositionVariation = POLY[modela] sherpa> fwhmVariation = POLY[modelaa] sherpa> modelb.pos => PositionVariation sherpa> modelb.fwhm => fwhmVariationThis example creates two different model stacks, and assigns the names PositionVariation and fwhmVariation to the model stacks. These model stack names are then used in parameter expressions, to link different parameters of modelb to different model components: the command modelb.fwhm => fwhmVariation, for example, links the parameter fwhm of modelb to the model component modelaa (via the model stack name fwhmVariation).
sherpa> SHLOGE[modelk]
sherpa> independent = SIN[modeli] + COS[modelj]
sherpa> SOURCE = modelk{independent}
The command SHLOGE[modelk] assigns the name modelk
to the Sherpa model component SHLOGE.
Next, the user assigns a model stack name (independent) to the model expression SIN[modeli] + COS[modelj].
With the final command, the user then assigns the model expression modelkindependent,
to the source model for dataset number 1.
This source model expression is a
nested model, which utilizes the
model stack. Note that the model stack definition is necessary since the following
syntax is not allowed:
Nested models define the function argument, on which a model expression is evaluated, to be another model expression.
A nested model, ![]() nested_model
nested_model![]() , appears as an element of a
model expression,
, appears as an element of a
model expression, ![]() modelExpr
modelExpr![]() ,
and is constructed using one of the following syntax options:
,
and is constructed using one of the following syntax options:
![]() sherpa_modelname
sherpa_modelname![]() {
{![]() model_stackname
model_stackname![]() }
}
![]() sherpa_modelname
sherpa_modelname![]() [
[![]() modelname
modelname![]() ]{
]{![]() model_stackname
model_stackname![]() }
}
![]() modelname
modelname![]() {
{![]() model_stackname
model_stackname![]() }
}
where ![]() model_stackname
model_stackname![]() must be enclosed in curly braces, { },
and where the
model stack
defines the
model expression for the function argument.
must be enclosed in curly braces, { },
and where the
model stack
defines the
model expression for the function argument.
See Section 5.4.7 Example 5, and Section 3, Example 3, for further examples.
sherpa> ERASE ALL
sherpa> oscillation = SIN
sherpa> SRC = SHLOGE{oscillation}
The user first assigns a
model stack name
to the Sherpa default model SIN.
The final command establishes the nested model, SHLOGE{oscillation}, and
assigns it to the
source model
for dataset number 1. This nested model
defines the function argument SIN,
over which the model component SHLOGE is
to be evaluated.
Note that the following syntax is not allowed:
sherpa> stackA = POLY
sherpa> stackB = GAUSS{stackA}
sherpa> SIN[modeli]
sherpa> SOURCE = modeli{stackB}
The command stackA = POLY creates the first model stack.
The next command creates a second model stack, using the nested model construction,
GAUSS{stackA}, where the function argument on which the
model component GAUSS is evaluated is the first model stack.
Finally, the source model expression is defined as the nested
model modeli{stackB} (i.e. modeli evaluated upon the second model stack).
Joint-mode models define the function argument, on which a model expression is evaluated, to be a particular data axis.
A joint-mode model, ![]() jointmode_model
jointmode_model![]() , may appear as an element of a
model expression,
, may appear as an element of a
model expression, ![]() modelExpr
modelExpr![]() ,
and is constructed using one of the following syntax options:
,
and is constructed using one of the following syntax options:
![]() sherpa_modelname
sherpa_modelname![]() {
{![]() axis
axis![]() }
}
![]() sherpa_modelname
sherpa_modelname![]() [
[![]() modelname
modelname![]() ]{
]{![]() axis
axis![]() }
}
![]() modelname
modelname![]() {
{![]() axis
axis![]() }
}
where ![]() axis
axis![]() must be enclosed in curly braces, { },
and where
must be enclosed in curly braces, { },
and where ![]() axis
axis![]() is a data column name.
Note that
is a data column name.
Note that ![]() axis
axis![]() defines the
particular data axis on which the model expression is to be evaluated.
defines the
particular data axis on which the model expression is to be evaluated.
See Section 5.4.7 Example 6 for an additional example.
sherpa> DATA example_img.fits FITSIMAGE
sherpa> LORENTZ[SpatialModelAxis0](98:5:200, 70:50:90, 1:1:200)
sherpa> POWLAW1D[SpecModelAxis1]
sherpa> SRC 1 = SpatialModelAxis0{x1}*SpecModelAxis1{x2}
The command LORENTZ[SpatialModelAxis0](98:5:200, 70:50:90, 1:1:200) assigns the name SpatialModelAxis0
to the Sherpa model component LORENTZ1D, and assigns various parameters values and
ranges. Similarly, a second model component is established and assigned a name.
The final command assigns the model expression SpatialModelAxis0{x1}*SpecModelAxis1{x2},
to the source model for dataset number 1. This source model expression is an algebraic
combination of joint-mode models, where these joint-mode models each define a specific data axis as the argument for
a model component. So with this source model expression, the joint-mode model SpatialModelAxis0{x1}
will fit model SpatialModelAxis0 to Axis 0 (x1) of the data, and the joint-mode model SpecModelAxis1{x2}
will jointly fit model SpecModelAxis1 to Axis 1 (x2) of the data, etc.
Model parameters may be frozen or thawed using one of the following equivalent commands:
sherpa> ![]() modelname
modelname![]() .
.![]() paramname
paramname![]() .TYPE = {FREEZE | THAW}
.TYPE = {FREEZE | THAW}
sherpa> ![]() modelname
modelname![]() .
.![]() #
#![]() .TYPE = {FREEZE | THAW}
.TYPE = {FREEZE | THAW}
sherpa> {FREEZE | THAW} ![]() modelname
modelname![]() .{
.{![]() paramname
paramname![]() |
| ![]() #
#![]() }
}
![]()
![]()
![]() modelname
modelname![]() .{
.{![]() paramname
paramname![]() |
| ![]() #
#![]() } ...
} ...![]()
In addition, all parameters of a model component may be frozen or thawed at once using:
sherpa> {FREEZE | THAW} ![]() modelname
modelname![]()
And, all parameters of a source model's components may be frozen or thawed at once using:
sherpa> {FREEZE | THAW} SOURCE ![]() #
#![]()
where # may specify the number of the dataset (default dataset number is 1).
With
parameter prompting on,
a model parameter may be frozen by
entering ![]()
![]() value
value![]() :
:![]() min
min![]() :
:![]() max
max![]()
![]() ,-1
at the model parameter value prompt,
where the -1 sets the parameter to be frozen.
(see Example 2, below).
,-1
at the model parameter value prompt,
where the -1 sets the parameter to be frozen.
(see Example 2, below).
See the FREEZE command and the THAW command for more information and further examples.
sherpa> PARAMPROMPT OFF sherpa> GAUSS[modelb] sherpa> modelb.ampl.TYPE = FREEZEThis command freezes the parameter ampl of modelb. The following commands are each equivalent:
sherpa> modelb.3.TYPE = FREEZE sherpa> FREEZE modelb.ampl sherpa> FREEZE modelb.3
sherpa> ERASE ALL
sherpa> PARAMPROMPT ON
Model parameter prompting is on
sherpa> GAUSS[modelb]
modelb.fwhm parameter value [10] 2,-1
modelb.pos parameter value [0] ,-1
modelb.ampl parameter value [1]
sherpa> SHOW modelb
gauss1d[modelb]
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 fwhm frozen 2 1.1755e-38 3.4028e+38
2 pos frozen 0-3.4028e+38 3.4028e+38
3 ampl thawed 1-3.4028e+38 3.4028e+38
In this example, parameters are frozen by entering
sherpa> PARAMPROMPT OFF
Model parameter prompting is off
sherpa> DATA data/example.pha
sherpa> GAUSS[modelc]
sherpa> SOURCE = modelb + modelc
sherpa> FREEZE modelc
sherpa> SHOW SOURCE
(modelb + modelc)
gauss1d[modelb] (integrate: on)
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 fwhm frozen 2 1.1755e-38 3.4028e+38
2 pos frozen 0-3.4028e+38 3.4028e+38
3 ampl thawed 1-3.4028e+38 3.4028e+38
gauss1d[modelc] (integrate: on)
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 fwhm frozen 0.7113 0.0071 71.1283
2 pos frozen 0.9442 0.0276 14.5494
3 ampl frozen 0.0001 1.0564e-06 0.0106
sherpa> THAW SOURCE
sherpa> SHOW SOURCE
(modelb + modelc)
gauss1d[modelb] (integrate: on)
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 fwhm thawed 2 1.1755e-38 3.4028e+38
2 pos thawed 0-3.4028e+38 3.4028e+38
3 ampl thawed 1-3.4028e+38 3.4028e+38
gauss1d[modelc] (integrate: on)
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 fwhm thawed 0.7113 0.0071 71.1283
2 pos thawed 0.9442 0.0276 14.5494
3 ampl thawed 0.0001 1.0564e-06 0.0106
Note that the command FREEZE modelc freezes all parameters of the source
model component modelc,
while THAW SOURCE thaws all parameters of both source
model components.
Parameter expressions are used to link model component parameters:
sherpa> ![]() CREATE
CREATE![]()
![]() modelname
modelname![]() .{
.{![]() paramname
paramname![]() |
| ![]() #
#![]() } =
} =![]()
![]() paramExpr
paramExpr![]()
where again ![]() modelname
modelname![]() is the name that has been given
to a model component by the user.
Note that either
is the name that has been given
to a model component by the user.
Note that either ![]() paramname
paramname![]() or
or ![]() #
#![]() may specify a parameter.
The parameter expression,
may specify a parameter.
The parameter expression, ![]() paramExpr
paramExpr![]() ,
to which the parameter is being linked,
may be composed of one, or more (combined algebraicly),
of the following elements:
,
to which the parameter is being linked,
may be composed of one, or more (combined algebraicly),
of the following elements:
| Element: | Description: |
|---|---|
| A model component parameter. | |
| A model expression, specified via a model stack name. |
A parameter expression may
be an algebraic combination of these elements that may include numerical
values and the following operators: + - * / ( ) ![]()
![]() {}.
{}.
The command UNLINK may be used to remove a link between model parameters:
sherpa> UNLINK ![]() modelname
modelname![]() .{
.{![]() paramname
paramname![]() |
| ![]() #
#![]() }
}
sherpa> ERASE ALL sherpa> PARAMPROMPT ON Model parameter prompting is on sherpa> GAUSS[modelb] modelb.fwhm parameter value [10] modelb.pos parameter value [0] modelb.ampl parameter value [1] sherpa> GAUSS[modelf] modelf.fwhm parameter value [10] modelf.pos parameter value [0] modelf.ampl parameter value [1] sherpa> modelf.ampl => 0.5*modelb.amplThe last command in this series uses a model parameter expression, to link the ampl parameter of modelf to 0.5 multiplied by the ampl parameter of modelb. That is, the amplitudes of two Gaussian models are linked, where one is half that of the other. Note that model parameter expressions cannot be created within the model parameter prompting. Note that the link may be removed as follows:
sherpa> UNLINK modelf.ampl
sherpa> PARAMPROMPT OFF Model parameter prompting is off sherpa> POW[modelc] sherpa> POW[modele] sherpa> modelc.1 => modele.1 sherpa> modelc.3 => 2*modele.3 - modele.3The next-to last command in this series links the first parameter (gamma) of modelc to the first parameter of modele. The last command in this series links the third parameter (ampl) of modelc to the parameter expression: 2 multiplied by the third parameter of modele, minus the third parameter of modele. Note that the links may be removed as follows:
sherpa> UNLINK modelc.1 sherpa> UNLINK modelc.3
sherpa> ERASE ALL sherpa> SIN[modeli] sherpa> SOURCE = modeli sherpa> PeriodVariation = POLY[modela] sherpa> modeli.period => PeriodVariationThe first command, SIN[modeli], assigns the name modeli to the Sherpa model component SIN. The second command defines this model component as the source model to be used for fitting. The third command, PeriodVariation = POLY[modela], creates a model stack. The final command links the parameter period of modeli to the parameter expression PeriodVariation (which is composed of the model component modela). Note that the following parameter expression syntax is currently not allowed:
The user can turn on and off the integration of non-XSPEC, non-instrument model components:
sherpa> ![]() modelname
modelname![]() INTEGRATE
INTEGRATE ![]() ON|OFF
ON|OFF![]()
Changing the integration status of a model component will only have an affect if binned data are being fit (e.g. PHA or histogram data).
The default integration status for each model is provided in Table 5.9, while the SHOW command can be used to determine whether a model component is currently being integrated.
The user must be careful not to define an unacceptable mixture of additive/integrated and multiplicative/non-integrated model components, such as by adding two model components with different integration statuses. Sherpa will issue a warning when it detects such an unacceptable mixture.
sherpa> POWLAW1D[p]
sherpa> SHOW p
powlaw1d[p] (integrate: on)
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 gamma thawed 0 -10 10
2 ref frozen 1-3.4028e+38 3.4028e+38
3 ampl thawed 1 1e-20 3.4028e+38
sherpa> p INTEGRATE OFF
sherpa> SHOW p
powlaw1d[p] (integrate: off)
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 gamma thawed 0 -10 10
2 ref frozen 1-3.4028e+38 3.4028e+38
3 ampl thawed 1 1e-20 3.4028e+38
| Description | Integration | |
|---|---|---|
| ATTEN | Attenuation by ISM. | OFF |
| BBODY | BB | Blackbody as a function of energy. | ON |
| BBODYFREQ | Blackbody as a function of frequency. | ON |
| BETA1D | 1-D surface brightness beta-model. | OFF |
| BETA2D | LORPOW2D | 2-D Lorentzian with varying power law. | ON |
| BOX1D | 1-D box function. | OFF |
| BOX2D | 2-D box function. | OFF |
| BPL1D | Broken power law function. | ON |
| CONST1D | CONST | 1-D constant amplitude model. | ON |
| CONST2D | 2-D constant amplitude model. | ON |
| COS | Cosine function. | OFF |
| DELTA1D | 1-D delta function. | ON |
| DELTA2D | 2-D delta function. | ON |
| DEVAUCOULEURS | DeVaucouleurs profile. | ON |
| DERED | Dereddening function. | OFF |
| EDGE | Photoabsorption edge model. | OFF |
| ERF | A 1-D error function. | OFF |
| ERFC | A 1-D complementary error function. | OFF |
| FARF1D | FARF | A 1-D file-based ancillary response model | N/A |
| FARF2D | FEXPMAP | FEXPMAP2D | A 2-D file-based ancillary response model | N/A |
| FPSF1D | A 1-D file-based PSF instrument model | N/A |
| FPSF2D | FPSF | PSFFROMFILE | A 2-D file-based PSF instrument model | N/A |
| FRMF1D | FRMF | A 1-D file-based response matrix model | N/A |
| GAUSS1D | GAUSS | 1-D unnormalized Gaussian function. | ON |
| GAUSS2D | 2-D unnormalized Gaussian function. | ON |
| GRIDMODEL | N-D user-specified amplitude model. | OFF |
| HIGHPASS | STEPHI1D | 1-D step function. | OFF |
| HUBBLE | REYNOLDS | Hubble-Reynolds profile. | ON |
| JDPILEUP | John Davis (MIT) pileup model. | OFF |
| KERNEL | A 1-D convolution model. | N/A |
| LINEBROAD | Line broadening profile. | ON |
| LORENTZ1D | LORENTZ | 1-D normalized Lorentzian function. | ON |
| LORENTZ2D | 2-D unnormalized Lorentzian function. | ON |
| LORPOW2D | BETA2D | 2-D Lorentzian with varying power law. | ON |
| LOWPASS | STEPLO1D | 1-D step function. | OFF |
| NBETA | 1-D normalized beta function. | ON |
| NGAUSS1D | 1-D normalized Gaussian function. | ON |
| PILEUP | 1-D pileup model function. | N/A |
| POISSON | Poisson function. | OFF |
| POLYNOM1D | POLY | 1-D polynomial function. | ON |
| POLYNOM2D | 2-D polynomial function. | ON |
| POWLAW1D | 1-D power law. | ON |
| PTSRC1D | A 1-D file-based point-source fitting model | OFF |
| PTSRC2D | PTSRC | A 2-D file-based point-source fitting model | OFF |
| REYNOLDS | HUBBLE | Hubble-Reynolds profiles. | ON |
| RSP1D | RSP | A 1-D instrument model. | N/A |
| RSP2D | A 2-D instrument model. | N/A |
| SCHECHTER | Schechter function. | OFF |
| SHEXP10 | Exponential function, base 10. | OFF |
| SHEXP | Exponential function. | OFF |
| SHLOG10 | Logarithm function, base 10. | OFF |
| SHLOGE | SHLOG | Natural logarithm function. | OFF |
| SIN | Sine function. | OFF |
| SQRT | Square root function. | OFF |
| STEPHI1D | HIGHPASS | 1-D step function. | OFF |
| STEPLO1D | LOWPASS | 1-D step function. | OFF |
| TAN | Tangent function. | OFF |
| TPSF1D | A 1-D TCD-model-based PSF instrument model | N/A |
| TPSF2D | TPSF |PSFFROMTCD | PSF | A 2-D TCD-model-based PSF instrument model | N/A |
| USERMODEL | User implemented model. | OFF |
| XS |
An XSPEC model function. | N/A |
The last column in Table 5.9
indicates whether the model is integrated by default when fit to binned data:
ON indicates that the model is integrated by default.
In section 5.4.13, we describe
the INTEGRATE ![]() ON|OFF
ON|OFF![]() command, which allows the
user to change the integration status of a non-XSPEC,
non-instrument model components.
command, which allows the
user to change the integration status of a non-XSPEC,
non-instrument model components.
In the remainder of this chapter, we describe each of the models listed above,
in alphabetical order.
Each model section includes a description of the
model, and a table listing of the model parameters. The listing of model
parameters includes the Sherpa parameter number, and the corresponding
Sherpa parameter name (![]() paramname
paramname![]() ).
).
Attenuation by ISM. Integration OFF.
This model calculates the transmission of the interstellar medium using the description of the ISM absorption of Rumph, Bowyer, & Vennes 1994, AJ 107, 2108. It includes neutral He autoionization features. Between 1.2398 and 43.655 Angstroms (i.e. in the 0.28-10 keV range) the model also accounts for metals as described in Morrison & MacCammon 1983, ApJ 270, 119.
The code uses the best available photoionization cross-sections to date from the atomic data literature and combines them in an arbitrary mixture of the three ionic species: HI, HeI, and HeII.
The model assumes that the data are expressed in Angstroms.
This model provided courtesy of Pat Jelinsky.
| Number | Name | Description |
|---|---|---|
| 1 | hcol | N(HI) column (atoms
|
| 2 | heiRatio | N(HeI)/N(HI) |
| 3 | heiiRatio | N(HeII)/N(HI) |
Blackbody as a function of energy. Integration ON.
Blackbody emission calculated as a function of energy using the expression:
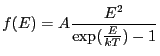 |
(5.2) |
where ![]() is the photon energy, and
is the photon energy, and
![]() is the
blackbody temperature (expressed in the same units as the photon energy).
The amplitude
is the
blackbody temperature (expressed in the same units as the photon energy).
The amplitude
![]() is related to the ratio of source radius to distance:
is related to the ratio of source radius to distance:
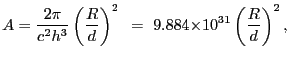 |
(5.3) |
with Planck's constant ![]() specified in keV-s and
the speed of light
specified in keV-s and
the speed of light ![]() specified in cm/s, and with
specified in cm/s, and with
![]() and
and ![]() representing the
radius of, and distance to, the source respectively. If
representing the
radius of, and distance to, the source respectively. If
![]() , while if
, while if
![]() .
.
| Number | Name | Description |
|---|---|---|
| 1 | space | 0: energy |
| 2 | kT | temperature |
| 3 | ampl | amplitude |
Blackbody as a function of frequency. Integration ON.
Blackbody emission calculated as a function of
![]() using Wien's law (
using Wien's law (
![]() ):
):
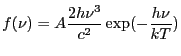 |
(5.4) |
where ![]() is the amplitude,
is the amplitude, ![]() is the temperature in Kelvin, and
is the temperature in Kelvin, and
![]() are Planck's constant, the speed of
light, and Boltzmann's constant, respectively.
are Planck's constant, the speed of
light, and Boltzmann's constant, respectively.
| Number | Name | Description |
|---|---|---|
| 1 | T | temperature |
| 2 | ampl | amplitude |
1-D surface brightness beta-model. Integration OFF
1-D surface brightness beta-model:
![$\displaystyle f(x) = A\left(1 + \left[\frac{x-x_o}{r_o}\right]^2\right)^{-3{\beta}+\frac{1}{2}}$](img159.gif) |
(5.5) |
| Number | Name | Description |
|---|---|---|
| 1 | r_o | core radius |
| 2 | beta | |
| 3 | xpos | offset |
| 4 | ampl | amplitude |
2-D Lorentzian with varying power law. Integration OFF. The LORPOW2D model is equivalent.
A 2-D Lorentz model with a varying power law, also known as a Beta model:
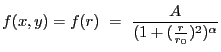 |
(5.6) |
where
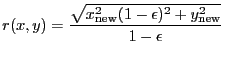 |
(5.7) |
| (5.8) |
and
| (5.9) |
| Number | Name | Description |
|---|---|---|
| 1 | r0 | core radius |
| 2 | xpos | x mean position |
| 3 | ypos | y mean position |
| 4 | ellip | ellipticity |
| 5 | theta | angle of ellipticity |
| 6 | ampl | amplitude |
| 7 | alpha | power law index |
1-D box function. Integration OFF.
A 1-D box model:
| (5.10) |
| (5.11) |
| Number | Name | Description |
|---|---|---|
| 1 | xlow | low cut-off
|
| 2 | xhi | high cut-off
|
| 3 | ampl | amplitude |
2-D box function. Integration OFF.
A 2-D box model:
| (5.12) |
if
![]() and
and
![]() ,
,
| (5.13) |
| Number | Name | Description |
|---|---|---|
| 1 | xlow | low x cut-off
|
| 2 | xhi | high x cut-off
|
| 3 | ylow | low y cut-off
|
| 4 | yhi | high y cut-off
|
| 5 | ampl | amplitude |
Broken power law function. Integration ON.
A broken power-law model:
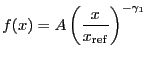 |
(5.14) |
if
![]() , and
, and
 |
(5.15) |
otherwise, where
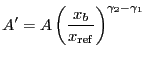 |
(5.16) |
| Number | Name | Description |
|---|---|---|
| 1 | gamma1 | first power law photon index |
| 2 | gamma2 | second power law photon index |
| 3 | eb | break-point |
| 4 | ref | normalization reference point |
| 5 | ampl | amplitude |
1-D constant amplitude model. Integration ON.
A 1-D constant amplitude model:
| (5.17) |
A is limited to being ![]() . To model
negative constant amplitudes, multiple by -1 in Sherpa:
. To model
negative constant amplitudes, multiple by -1 in Sherpa:
sherpa> source = (-1)*const[cs]
| Number | Name | Description |
|---|---|---|
| 1 | c0 | amplitude |
2-D constant amplitude model. Integration ON.
A 2-D constant amplitude model:
| (5.18) |
| Number | Name | Description |
|---|---|---|
| 1 | c0 | amplitude |
Cosine function. Integration OFF.
A 1-D cosine model:
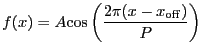 |
(5.19) |
| Number | Name | Description |
|---|---|---|
| 1 | period | period |
| 2 | offset | x offset
|
| 3 | ampl | amplitude |
1-D delta function. Integration ON.
A 1-D delta-function model:
| (5.20) |
| (5.21) |
with
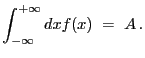 |
(5.22) |
| Number | Name | Description |
|---|---|---|
| 1 | pos | position |
| 2 | ampl | amplitude |
2-D delta function. Integration ON.
A 2-D delta-function model:
| (5.23) |
if ![]() and
and ![]() ,
,
and,
| (5.24) |
with
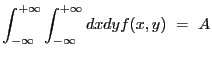 |
(5.25) |
| Number | Name | Description |
|---|---|---|
| 1 | xpos | x position |
| 2 | ypos | y position |
| 3 | ampl | amplitude
|
Dereddening function. Integration OFF.
This dereddening model uses the analytic formula for the mean extension law described in Cardelli, Clayton, & Mathis 1989, ApJ 345, 245:
| (5.26) |
where
![]() is the
wavelength-dependent optical depth,
is the
wavelength-dependent optical depth,
| (5.27) |
and ![]() and
and ![]() are computed
using wavelength-dependent formulae which we will not reproduce here,
for the wavelength range 1000
Å - 3.3
microns. The relationship between the color excess and the column
density is
are computed
using wavelength-dependent formulae which we will not reproduce here,
for the wavelength range 1000
Å - 3.3
microns. The relationship between the color excess and the column
density is
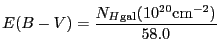 |
(5.28) |
(Bohlin, Savage, & Drake 1978, ApJ 224, 132). The value of the
ratio of total to selective extinction, ![]() ,
is initially set to 3.1, the standard value for the diffuse ISM. The
final model form is:
,
is initially set to 3.1, the standard value for the diffuse ISM. The
final model form is:
![$\displaystyle I(\lambda) = I(0) \exp\left [-\frac{N_{H{\rm gal}} \left[a R_v + b\right]}{58.0 \times 1.086}\right]$](img207.gif) |
(5.29) |
This model should only be used as a multiplicative model:
sherpa> powlaw1d[con1](1.,2588.6,0.1) sherpa> dered[dr](3.1,0.1) sherpa> source 1 = con1*dr
This model provided courtesy of Karl Forster.
| Number | Name | Description |
|---|---|---|
| 1 | rv | total to selective extinction ratio |
| 2 | nhgal | absorbing column density
|
DeVaucouleurs profile. Integration OFF.
A 2-D de Vaucouleurs model:
![$\displaystyle f(x,y) = f(r) = A\exp\left[-7.67\left(\sqrt{\left[\frac{x_{\rm ma...
...ght]^2 + \left[\frac{x_{\rm min}}{r_{\rm min}}\right]^2}\right)^{0.25}-1\right]$](img209.gif) |
(5.30) |
where
| (5.31) |
| (5.32) |
| (5.33) |
| (5.34) |
| Number | Name | Description |
|---|---|---|
| 1 | r0 | core radius |
| 2 | xpos | x mean position |
| 3 | ypos | y mean position |
| 4 | ellip | ellipticity |
| 5 | theta | angle of ellipticity |
| 6 | ampl | amplitude |
Photoabsorption edge model. Integration OFF.
A phenomenological photoabsorption edge model as a function of energy:
| (5.35) |
if ![]() , and
, and
![$\displaystyle f(x) \exp\left[-A\left(\frac{x}{E_b}\right)^{-3}\right]$](img218.gif) |
(5.36) |
otherwise.
Or, as a function of wavelength:
| (5.37) |
if
![]() , and
, and
![$\displaystyle = f(x) \exp\left[-A\left(\frac{x}{{\lambda}_b}\right)^3\right]$](img220.gif) |
(5.38) |
otherwise.
| Number | Name | Description |
|---|---|---|
| 1 | space | energy (0) or wavelength (1) |
| 2 | thresh | edge position |
| 3 | abs | absorption coefficient |
A 1-D error function. Integration OFF.
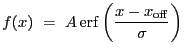 |
(5.39) |
where
![$\displaystyle \mathrm{erf}(y)~=~\frac{2}{\sqrt\pi}\,\int_{0}^{y}\exp\left[-t^2\right]dt$](img224.gif) |
(5.40) |
| Number | Name | Description |
|---|---|---|
| 1 | ampl | amplitude |
| 2 | offset | offset
|
| 3 | sigma | scaling factor |
erf is related to erfc, a complementary error function:
erfc(y) = 1 - erf(y)
See ERFC for information on that function.
A 1-D complementary error function. Integration OFF.
 |
(5.41) |
where
![$\displaystyle \mathrm{erfc}(y)~=~\frac{2}{\sqrt\pi}\,\int_{y}^{\infty}\exp\left[-t^2\right]dt$](img226.gif) |
(5.42) |
| Number | Name | Description |
|---|---|---|
| 1 | ampl | amplitude |
| 2 | offset | offset
|
| 3 | sigma | scaling factor |
erfc is related to erf, a 1-D error function:
erfc(y) = 1 - erf(y)
See ERF for information on that function.
A 1-D file-based ancillary response model.
FARF is a file-based ARF model that represents an ancillary response vector (e.g., the effective area as a function of energy/wavelength).
Note that in Sherpa analyses, the energy-space binning of the ARF (found typically in the ENERG_LO and ENERG_HI columns of the SPECRESP extension of the ARF file) does not have to match the analogous energy-space binning of a matching RMF. (This is also true if instead of energy, the ARF is defined as a function of wavelength.)
See the documentation on the INSTRUMENT command. See also the RSP and FRMF instrument models.
| Number | Name | Description |
|---|---|---|
| 1 | arf | ARF file name |
| 2 | norm | normalization |
A 2-D file-based ancillary response model. Alternate names include FEXPMAP and FEXPMAP2D.
FARF2D is a file-based model whose primary use is
to represent 2-D exposure maps in arbitrary units (seconds,
![]() , etc.).
, etc.).
Note the following about exposure maps:
See the documentation on the INSTRUMENT command. See also the RSP2D instrument model.
| Number | Name | Description |
|---|---|---|
| 1 | file | exposure map file name |
| 2 | norm | normalization |
Examples:
Input an exposure map for use with a dataset:
sherpa> DATA data/data.fits sherpa> PARAMPROMPT OFF Model parameter prompting is off sherpa> FEXPMAP[emap] sherpa> emap.file = "data/data_expmap.fits" sherpa> INSTRUMENT = emap
In this example, the instrument model component FEXPMAP is established, the exposure map file is input using this model's file parameter, and the instrument model stack is set for dataset number 1.
The CIAO 2.3 equivalent of this command is:
sherpa> DATA data/data.fits sherpa> PARAMPROMPT OFF Model parameter prompting is off sherpa> GRIDMODEL[gm] sherpa> gm.file = "data/data_expmap.fits" sherpa> EXPMAP 1 = gm
Use a point-spread function file in addition to an exposure map:
sherpa> FEXPMAP[emap] sherpa> emap.file = "data/data_expmap.fits" sherpa> FPSF[psfunc] sherpa> psfunc.file = "data/data_psf.fits" sherpa> INSTRUMENT = emap*psfunc
This may also be done with the RSP2D command:
sherpa> RSP2D[r] sherpa> r.empfile = "data/data_expmap.fits" sherpa> r.psffile = "data/data_psf.fits" sherpa> INSTRUMENT = r
A 1-D file-based PSF instrument model.
FPSF1D is a file-based PSF model that represents the point-spread function, a redistribution function that maps photon locations to data bins.
This model cannot be used in a source model expression. See PTSRC1D model if you want to fit the data with the PSF model file.
ASCII and FITS formats are allowed for the input model file . The current implementation requires that the bin size of the data and the PSF model file are the same. The number of bins can be different.
Note that the input file is automatically renormalized to 1 upon entry. Renormalization is done by summing over all bins, regardless of the setting of xsize.
The input PSF array is used to convolve (fold) a given source
model. This convolution can be performed using either Fast Fourier
Transforms (FFTs, the default), or the sliding cell technique
(see the parameter fft). If the axis length is
![]() and the length of the kernel axis is
and the length of the kernel axis is
![]() ,
then the computation time for the sliding cell goes as
,
then the computation time for the sliding cell goes as
![]() , i.e., for large
kernels the best choice is using the FFT. A rough rule-of-thumb for
1-D fits is to use the FFT if
, i.e., for large
kernels the best choice is using the FFT. A rough rule-of-thumb for
1-D fits is to use the FFT if
![]() .
.
"xsize" parameter defines the number of bins extracted from the file to be used in the PSF model.
xoff ![]() 0, the PSF (kernel) sub-array is extracted
from the center of the original array contained
in the input PSF file.
0, the PSF (kernel) sub-array is extracted
from the center of the original array contained
in the input PSF file.
Note that the kernel centroid must always be at the center of the extracted sub-array! Otherwise, systematic shifts will occur in best-fit positions of point sources.
In Sherpa version 3.0.2, a new parameter is introduced: radial. If set to 1 the kernel array will be extended and its values reflected across the edge boundary. The resultant function will be symmetric. The default value is 0.
See the documentation on the INSTRUMENT command.
| Number | Name | Description |
|---|---|---|
| 1 | file | input file name (FITS or ASCII) |
| 2 | xsize | x-full-width of the subset region of kernel file to use in convolution |
| 3 | xoff | x-direction offset |
| 4 | fft | convolution type: 1 |
| 5 | radial | radial profile: 1 |
Examples:
The example below shows the initial parameter values for the FPSF1D model. Note that the default xsize value is set to 32 before the PSF data file is read in. After reading the data file the xsize is set to the size of the array in the model file.
sherpa> fpsf1d[psf0]
sherpa> show psf0
fpsf1d[psf0]
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 file string: "none"
2 xsize frozen 32 1 1024
3 xoff frozen 0 -512 512
4 fft frozen 1 0 1
5 radial frozen 0 0 1
sherpa> psf0.file=test_model.dat
sherpa> show psf0
fpsf1d[psf0]
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 file string: "test_model.dat"
2 xsize frozen 38 1 38
3 xoff frozen 0 -19 19
4 fft frozen 1 0 1
5 radial frozen 0 0 1
sherpa> instrument = psf0
A 2-D file-based PSF instrument model.
FPSF is a file-based PSF model that represents the point-spread function, a redistribution function that maps photon spatial locations to image bins.
The input PSF FITS image is used to convolve (fold) a given source
model. This convolution can be performed using either Fast Fourier
Transforms (FFTs, the default), or the sliding cell technique
(see the parameter fft). If the length of one axis is
![]() and the length of the kernel axis is
and the length of the kernel axis is
![]() ,
then the computation time for the sliding cell goes as
,
then the computation time for the sliding cell goes as
![]() , i.e., for large
kernels the best choice is using the FFT. A rough rule-of-thumb for
2-D fits is to use the FFT if
, i.e., for large
kernels the best choice is using the FFT. A rough rule-of-thumb for
2-D fits is to use the FFT if
![]() .
.
Note that the PSF is automatically renormalized upon entry. Renormalization is done by summing over all image pixels, regardless of the setting of xsize and ysize.
The following example will serve to clarify the meanings of the remaining parameters.
Assume that the PSF is provided in a FITS image (file) of
size
![]() .
. ![]() and
and ![]() may be much larger
than the PSF size in bins.
An optimally sized sub-image of size
(
may be much larger
than the PSF size in bins.
An optimally sized sub-image of size
(
![]() can be extracted and used in the PSF
convolution process.
can be extracted and used in the PSF
convolution process.
If xoff ![]() yoff
yoff ![]() 0, the kernel sub-image is extracted
from the center of the original image contained in file.
The user may find that changing xoff and/or
yoff can result in his or her being able to extract a
smaller optimally sized sub-image if, say, the PSF is too asymmetric
to be fit easily into a centered rectangle. Note that actual PSF image
may be outside the default extracted PSF image.
0, the kernel sub-image is extracted
from the center of the original image contained in file.
The user may find that changing xoff and/or
yoff can result in his or her being able to extract a
smaller optimally sized sub-image if, say, the PSF is too asymmetric
to be fit easily into a centered rectangle. Note that actual PSF image
may be outside the default extracted PSF image.
Note that the kernel centroid must always be at the center of the extracted sub-image! Otherwise, systematic shifts will occur in best-fit positions of point sources, etc.
See the documentation on the INSTRUMENT command.
| Number | Name | Description |
|---|---|---|
| 1 | file | input FITS file name |
| 2 | xsize | x-width of the subset region of kernel PSF file to use in convolution |
| 3 | ysize | y-width of the subset region of kernel PSF file to use in convolution |
| 4 | xoff | x-direction offset |
| 5 | yoff | y-direction offset |
| 6 | fft | convolution type: 1 |
A 1-D file-based response matrix model.
FRMF is a file-based RMF model that represents the redistribution matrix which maps photon energy to, e.g., PHA bin.
Note that in Sherpa analyses, the energy-space binning of the RMF (found typically in the ENERG_LO and ENERG_HI columns of the MATRIX extension of the RMF file) does not have to match the analogous energy-space binning of a matching ARF. (This is also true if instead of energy, the RMF is defined as a function of wavelength.)
See the documentation on the INSTRUMENT command. See also the RSP and FARF1D instrument models.
| Number | Name | Description |
|---|---|---|
| 1 | rmf | RMF file name |
1-D unnormalized Gaussian function. Integration ON.
An unnormalized 1-D Gaussian model:
![$\displaystyle f(x) = A\exp\left[-f\left(\frac{x-x_{\rm o}}{F}\right)^{2}\right]$](img236.gif) |
(5.43) |
The constant ![]()
![]() 2.7725887
2.7725887 ![]() 4log2 relates the
full-width at half-maximum
4log2 relates the
full-width at half-maximum ![]() to the Gaussian
to the Gaussian
![]() so that F
so that F![]() sqrt(8log2)*sigma.
sqrt(8log2)*sigma.
See also the 1-D normalized Gaussian function, NGAUSS1D.
| Number | Name | Description |
|---|---|---|
| 1 | fwhm | full-width at half-maximum |
| 2 | pos | mean position |
| 3 | ampl | amplitude |
2-D unnormalized Gaussian function. Integration OFF.
A 2-D Gaussian model:
![$\displaystyle f(x,y) = f(r) = A\exp\left[-f\left(\frac{r}{F}\right)^2\right]$](img238.gif) |
(5.44) |
where
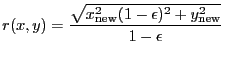 |
(5.45) |
| (5.46) |
and
| (5.47) |
The constant ![]()
![]() 2.7725887
2.7725887 ![]() 4log2 relates the
full-width at half-maximum
4log2 relates the
full-width at half-maximum ![]() to the Gaussian
to the Gaussian
![]() .
.
| Number | Name | Description |
|---|---|---|
| 1 | fwhm | full-width at half-maximum |
| 2 | xpos | x mean position |
| 3 | ypos | y mean position |
| 4 | ellip | ellipticity |
| 5 | theta | angle of ellipticity |
| 6 | ampl | amplitude |
N-D user-specified amplitude model. Integration OFF.
| Number | Name | Description |
|---|---|---|
| 1 | file | input filename |
| 2 | norm | normalization |
With GRIDMODEL, an N-dimensional data array may be input and used directly as a model. The data array must be of the same size as the source data and have the same binning.
Prior to CIAO 3.0, it was necessary to use GRIDMODEL when inputting an exposure map for use in spatial fitting; this is no longer true. Example 2 compares the CIAO 3.0 and 2.3 syntax; see the FEXPMAP command for further information.
Examples:
Input a data array as a model:
sherpa> PARAMPROMPT OFF Model parameter prompting is off sherpa> GRIDMODEL[gm] sherpa> gm.file = "data/example1.dat" sherpa> THAW gm.norm sherpa> SOURCE = gm
In this example, the model component GRIDMODEL is established and assigned the name gm. Then, the input data array file is input using this model's file parameter. This model component, thus defined using an input data array, can then be used just as any other model component may be used. For example, here the model's normalization is thawed and then the model is used to define a source model expression for fitting.
Input an exposure map for use with a dataset (this no longer uses the GRIDMODEL command):
sherpa> DATA data/data.fits sherpa> PARAMPROMPT OFF Model parameter prompting is off sherpa> FEXPMAP[emap] sherpa> emap.file = "data/data_expmap.fits" sherpa> INSTRUMENT = emap
In this example, the instrument model component FEXPMAP is established, the exposure map file is input using this model's file parameter, and the instrument model stack is set for dataset number 1.
The CIAO 2.3 equivalent of this command is:
sherpa> DATA data/data.fits sherpa> PARAMPROMPT OFF Model parameter prompting is off sherpa> GRIDMODEL[gm] sherpa> gm.file = "data/data_expmap.fits" sherpa> EXPMAP 1 = gm
1-D step function. Integration OFF. The command HIGHPASS is equivalent.
A 1-D step model:
and
| (5.48) |
| Number | Name | Description |
| 1 | xcut | cut-off x_cut |
| 2 | ampl | amplitude A |
Hubble-Reynolds profile. Integration OFF. The REYNOLDS model is equivalent.
A 2-D Hubble-Reynolds model:
![$\displaystyle f(x,y)~=~f(r)~=~\frac{A}{\left[\sqrt{\left(\frac{x_{\rm maj}}{r_{\rm maj}}\right)^2+\left(\frac{x_{\rm min}}{r_{\rm min}}\right)^2} + 1\right]^2 }$](img241.gif) |
(5.49) |
where
| (5.50) |
| (5.51) |
| (5.52) |
and
| (5.53) |
| Number | Name | Description |
|---|---|---|
| 1 | r0 | core radius |
| 2 | xpos | x mean position |
| 3 | ypos | y mean position |
| 4 | ellip | ellipticity |
| 5 | theta | angle of ellipticity |
| 6 | ampl | amplitude |
A CCD pileup model developed by John Davis of MIT.
The 1D pileup model can be applied to model the 1D Chandra spectrum obtained in the imaging mode. It should not be used for Chandra grating or 2D image data. This model is used for fitting energy spectra only.
Subsequent use of Powell and Simplex optimization methods is desirable when fitting data with pileup model.
Several model parameters describe pileup:
n, f and g0: The values of n, f and g0 should remain frozen; The full discussion of these parameters is presented in Davis (2001).
alpha:
The value of the parameter alpha should be allowed to vary. alpha parameterizes "grade migration" in the detector, and represents the probability, per photon count greater than one, that the piled event is not rejected by the spacecraft software as a "bad event". Specifically, if n photons are piled together in a single frame, the probability of them being retained (as a single photon event with their summed energy) is given by alpha(n-1). In reality, the alpha parameter should be a photon-energy-dependent and detector-chip-dependent matrix; for simplicity, the jdpileup model assumes a constant value.
ftime:
The ftime and parameter should be set to the value given in the header keyword EXPTIME of the event file. (Note that EXPTIME is used instead of TIMEDEL because the latter includes the transfer time, which ftime should not.)
fracexp:
The fracexp parameter should be set to the value given in the header keyword FRACEXPO of the ARF file:
| Number | Name | Description |
|---|---|---|
| 1 | alpha | grade migration; probability of a good grade when two photons pile together |
| 2 | g0 | probability of grade 0 assignment |
| 3 | f | fraction of flux falling into the pileup region |
| 4 | n | number of detection cells |
| 5 | ftime | frame time
|
| 6 | fracexp | fractional exposure that the point source experienced while dithering on the chip (keyword FRACPROB in the ARF file) |
The pileup model does not work for pileup in dispersed grating spectra. The model was designed for imaging pileup, including pileup by the gratings in zeroth order.
For more information, see the Sherpa thread on Using a Pileup Model and the Event Pileup in Charge Coupled Devices page by John E. Davis.
Examples:
This example illustrate the setting of the pileup model.
sherpa> DATA spectrum.pi
sherpa> INSTRUMENT = RSP[myinst]("source.rmf", "source.arf")
sherpa> POW[p]
sherpa> SOURCE = p
sherpa> JDPILEUP[jdp]
sherpa> PILEUP = jdp
sherpa> show jdp
jdpileup[jdp] (integrate: off)
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 alpha thawed 0.5 0 1
2 g0 frozen 1 1e-120 1
3 f thawed 0.95 0.9 1
4 n frozen 1 1e-120 100
5 ftime frozen 3.241 1e-120 5 sec
6fracexp frozen 0.987 0 1
sherpa> fit
In this example, data is input and a power-law
model component is established and
then defined as the source model for fitting. The command
JDPILEUP![]() jdp
jdp![]() establishes the
JDPILEUP model component and assigns it the name
jdp.
The command
PILEUP
establishes the
JDPILEUP model component and assigns it the name
jdp.
The command
PILEUP ![]() jdp then defines this pileup model for use in fitting.
jdp then defines this pileup model for use in fitting.
After fitting, display the pileup fractions with SHOW PILEUP:
sherpa> SHOW PILEUP 1: 0.224696 0.541445 2: 0.263513 0.304025 3: 0.206024 0.113808 4: 0.120808 0.031952 5: 0.0566711 0.00717652 6: 0.0221538 0.00134322 7: 0.00742312 0.000215494 8: 0.00217637 3.02503e-05 9: 0.000567189 3.77462e-06 10: 0.000133035 4.23895e-07 *** pileup fraction: 0.458555
Each row represents the number of photons per CCD frame. The maximum number of rows is 20; here, there were no more than 10 photons piled together per frame. The left column represents the percentage of frames with the stated number of photons: here, 22.47% of frames contained a single photon, 26.35% contained two photons piled together, etc. The right column indicates the percentage of observed counts with the stated number of photons: here, 54.14% of recorded counts were comprised of one photon, etc.. The total pileup fraction is the sum of the right column, excluding the first row: here, 45.85% of observed counts actually contain two or more photons piled together.
Defines an expression to be used as a kernel in 1D source model convolution.
sherpa> KERNEL [<dataset range> | ALLSETS [ID]] = <modelExpr>
![]() dataset range
dataset range![]()
![]() # (or more generally #:#,#:#, etc.) such that
# specifies a dataset number and #:# represents an inclusive range of datasets;
one may specify multiple inclusive ranges by separating them with
commas. The default dataset is dataset 1.
# (or more generally #:#,#:#, etc.) such that
# specifies a dataset number and #:# represents an inclusive range of datasets;
one may specify multiple inclusive ranges by separating them with
commas. The default dataset is dataset 1.
The model expression,
![]() modelExpr
modelExpr![]() ,
is an algebraic combination of one or more of the following elements:
,
is an algebraic combination of one or more of the following elements:
{<sherpa_modelname> | <sherpa_modelname>[modelname] |
<modelname> | <model_stack> | <nested_model>}
along with numerical values. The following operators are
recognized: ![]() - * / ( ) { }.
See the CREATE command for further information.
- * / ( ) { }.
See the CREATE command for further information.
Note that:
To reset the kernel model stack, issue the command:
sherpa> KERNEL [<dataset range> | ALLSETS] =
The KERNEL model stack is used to convolve source model expressions. As such, it has many uses, of which two are the following:
Note that the parameter values of a KERNEL model stack are frozen in fits; the kernel shape cannot be optimized.
The KERNEL model stack is evaluated on the same data grid as the SOURCE model stack. In general, the data grid will not be the correct grid for convolution; in the case of Gaussian smoothing, the convolved spectrum may exhibit, e.g., spectral lines that are both dilated and translated. To prevent translation, the user must set an origin for the convolution kernel using the command:
sherpa> KERNEL.ORIGIN [<dataset range> | ALLSETS] = <coordinate>
The example below will help illustrate this point.
Examples:
Define SOURCE and KERNEL model stacks; define the origin of the convolution kernel; and fit:
sherpa> SOURCE = GAUSS[modela]
modela.fwhm parameter value [19.3451]
modela.pos parameter value [804]
modela.ampl parameter value [126]
sherpa> KERNEL = NGAUSS[modelb]
modelb.fwhm parameter value [19.3451] 20
modelb.pos parameter value [804]
modelb.ampl parameter value [2594.62] 1:1:1
sherpa> KERNEL.ORIGIN = 804
sherpa> FIT
LVMQT: V2.0
LVMQT: initial statistic value = 578.346
LVMQT: final statistic value = 64.8424 at iteration 6
modela.fwhm 25.3426
modela.pos 807.882
modela.ampl 150.302
sherpa> KERNEL =
sherpa> FIT
LVMQT: V2.0
LVMQT: initial statistic value = 294.76
LVMQT: final statistic value = 64.3803 at iteration 7
modela.fwhm 32.3536
modela.pos 807.863
modela.ampl 117.826
The convolution kernel is a normalized Gaussian, with integrated area set to 1 and full-width half-max of 20. (For a normalized Gaussian, the integrated area equals the amplitude.) The kernel origin is set to be the centroid of the normalized Gaussian (modelb.pos). Note the differences in the values of modela.fwhm and modela.ampl between each fit.
Line broadening profile. Integration ON.
A line-broadening profile:
![$\displaystyle f(\lambda)~=~\frac{2 A c}{{\pi}{\lambda}v{\sin}i} \left[ 1 - \left( \frac{{\Delta}\lambda}{\lambda_{\rm rest}} \frac{c}{v{\sin}i} \right)^2 \right]$](img244.gif) |
(5.54) |
where
| (5.55) |
| Number | Name | Description |
|---|---|---|
| 1 | rest | rest wavelength
|
| 2 | vsini | rotation velocity |
| 3 | ampl | amplitude |
1-D normalized Lorentzian function. Integration ON.
A normalized 1-D Lorentz model:
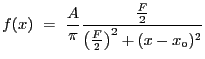 |
(5.56) |
with
 |
(5.57) |
| Number | Name | Description |
|---|---|---|
| 1 | fwhm | full-width at half-maximum |
| 2 | pos | mean position |
| 3 | ampl | amplitude |
2-D unnormalized Lorentzian function. Integration OFF.
An unnormalized 2-D Lorentz model:
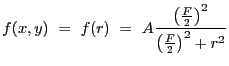 |
(5.58) |
where
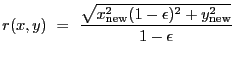 |
(5.59) |
| (5.60) |
and
| (5.61) |
| Number | Name | Description |
|---|---|---|
| 1 | fwhm | full-width at half-maximum |
| 2 | xpos | x mean position |
| 3 | ypos | y mean position |
| 4 | ellip | ellipticity |
| 5 | theta | angle of ellipticity |
| 6 | ampl | amplitude |
Another name for the BETA2D model. See Section 5.10.
1-D step function. Integration OFF. The command LOWPASS is equivalent.
A 1-D step model:
| (5.62) |
| (5.63) |
| Number | Name | Description |
| 1 | xcut | cut-off x_cut |
| 2 | ampl | amplitude A |
1-D normalized beta function. Integration ON.
A normalized 1-D beta function appropriate for use fitting line profiles:
![$\displaystyle f(x)~=~\frac{A}{\left[1 + \frac{(x-x_0)^2}{w^2}\right]^{-\alpha}}$](img253.gif) |
(5.64) |
| Number | Name | Description |
|---|---|---|
| 1 | pos | line centroid |
| 2 | width | line width |
| 3 | index | index |
| 4 | ampl | line amplitude |
1-D normalized Gaussian function. Integration ON.
A normalized 1-D Gaussian model:
![$\displaystyle f(x)~=~\frac{A}{\sqrt{\frac{\pi}{f}}F} \exp\left[-f\left(\frac{x-x_{\rm o}}{F}\right)^{2}\right]$](img256.gif) |
(5.65) |
with
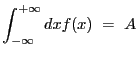 |
(5.66) |
The constant ![]()
![]() 2.7725887
2.7725887 ![]() 4log2 relates the
full-width at half-maximum
4log2 relates the
full-width at half-maximum ![]() to the Gaussian
to the Gaussian
![]() so that F
so that F![]() sqrt(8log2)*sigma.
sqrt(8log2)*sigma.
See also the 1-D unnormalized Gaussian function, GAUSS1D.
| Number | Name | Description |
|---|---|---|
| 1 | fwhm | full-width at half-maximum |
| 2 | pos | mean position |
| 3 | ampl | amplitude |
Defines the pileup model expression to be used for fitting a 1D dataset.
sherpa> PILEUP [<dataset range> | ALLSETS] = <pileupModelExpr>
![]() dataset range
dataset range![]()
![]() # (or more generally #:#,#:#, etc.) such that
# specifies a dataset number and #:# represents an inclusive range of datasets;
one may specify multiple inclusive ranges by separating them with
commas. The default dataset is dataset 1.
# (or more generally #:#,#:#, etc.) such that
# specifies a dataset number and #:# represents an inclusive range of datasets;
one may specify multiple inclusive ranges by separating them with
commas. The default dataset is dataset 1.
In CIAO 3.0 Sherpa, there is one pileup model available: JDPILEUP, developed by John Davis at MIT. The pileup model does not work for pileup in dispersed spectra. Rather, the model was designed for imaging pileup, including pileup by the gratings in zeroth order. This model is used for fitting energy spectra only.
Note that:
To reset the pileup model stack, issue the command:
sherpa> PILEUP [<dataset range> | ALLSETS] =
Examples:
Define a pileup model for use:
sherpa> DATA data/source.pi
The inferred file type is PHA. If this is not what you want, please
specify the type explicitly in the data command.
WARNING: statistical errors specified in the PHA file.
These are currently IGNORED. To use them, type:
READ ERRORS "<filename>[cols CHANNEL,STAT_ERR]" fitsbin
sherpa> PARAMPROMPT OFF
Model parameter prompting is off
sherpa> INSTRUMENT = RSP[myinst]("data/source.rmf", "data/source.arf")
The inferred file type is ARF. If this is not what you want, please
specify the type explicitly in the data command.
sherpa> POW[p]
sherpa> SOURCE = p
sherpa> JDPILEUP[jdp]
sherpa> PILEUP = jdp
sherpa> FIT
In this example, data is input and a power-law
model component is established and
then defined as the source model for fitting. The command
JDPILEUP![]() jdp
jdp![]() establishes the
JDPILEUP model component and assigns it the name
jdp.
The command
PILEUP
establishes the
JDPILEUP model component and assigns it the name
jdp.
The command
PILEUP ![]() jdp then defines this pileup model for use in fitting.
jdp then defines this pileup model for use in fitting.
After fitting, display the pileup fractions with SHOW PILEUP:
sherpa> SHOW PILEUP 1: 0.224696 0.541445 2: 0.263513 0.304025 3: 0.206024 0.113808 4: 0.120808 0.031952 5: 0.0566711 0.00717652 6: 0.0221538 0.00134322 7: 0.00742312 0.000215494 8: 0.00217637 3.02503e-05 9: 0.000567189 3.77462e-06 10: 0.000133035 4.23895e-07 *** pileup fraction: 0.458555
Each row represents the number of photons per CCD frame. The maximum number of rows is 20; here, there were no more than 10 photons piled together per frame. The left column represents the percentage of frames with the stated number of photons: here, 22.47% of frames contained a single photon, 26.35% contained two photons piled together, etc. The right column indicates the percentage of observed counts with the stated number of photons: here, 54.14% of recorded counts were comprised of one photon, etc.. The total pileup fraction is the sum of the right column, excluding the first row: here, 45.85% of observed counts actually contain two or more photons piled together.
Poisson function. Integration OFF.
A model expressing the ratio of two Poisson distributions of mean mu, one for which the random variable is x, and the other for which the random variable is equal to mu itself:
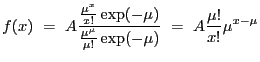 |
(5.67) |
| Number | Name | Description |
|---|---|---|
| 1 | mean | mean |
| 2 | ampl | amplitude |
1-D polynomial function. Integration ON.
A 1-D polynomial of order ![]() 8:
8:
 |
(5.68) |
where the coefficients ![]() are the parameters
numbered
are the parameters
numbered ![]() , and
, and
![]() is parameter number 10.
is parameter number 10.
Note that there is a degeneracy in the parameters, so it is
recommended to set at least one of ![]() or
or
![]() to zero and freeze it;
thawing both may lead to unpredicted results.
to zero and freeze it;
thawing both may lead to unpredicted results.
Note also that all coefficients except ![]() are
default frozen, so that the default polynomial model is a constant.
are
default frozen, so that the default polynomial model is a constant.
| Number | Name | Description |
|---|---|---|
| 1 | c0 | coefficient |
| 2 | c1 | coefficient |
| 3 | c2 | coefficient |
| 4 | c3 | coefficient |
| 5 | c4 | coefficient |
| 6 | c5 | coefficient |
| 7 | c6 | coefficient |
| 8 | c7 | coefficient |
| 9 | c8 | coefficient |
| 10 | offset | offset for x
|
2-D polynomial function. Integration ON.
A 2-D polynomial model of order ![]()
| (5.69) |
| Number | Name | Description |
|---|---|---|
| 1 | constant | constant coefficient |
| 2 | cx1 | coefficient
|
| 3 | cx2 | coefficient
|
| 4 | cy1 | coefficient
|
| 5 | cy2 | coefficient
|
| 6 | cx1y1 | coefficient
|
| 7 | cx1y2 | coefficient
|
| 8 | cx2y1 | coefficient
|
| 9 | cx2y2 | coefficient
|
1-D power law. Integration ON.
A 1-D power-law model:
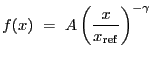 |
(5.70) |
The variable ![]() is assumed to be
is assumed to be ![]() .
.
| Number | Name | Description |
|---|---|---|
| 1 | gamma | power law photon index |
| 2 | ref | normalization reference point
|
| 3 | ampl | amplitude |
A 1-D file-based point-source fitting model.
PTSRC1D is a file-based model that may be used in fitting sources, to determine, e.g., if they are point-like or extended.
This model cannot be used as an instrument model.
ASCII and FITS formats are allowed for the input model file . The current implementation requires that the bin size of the data and the PTSRC1D model file are the same. The number of bins can be different.
The model has several parameters, which can be used to adjust the model array to be used in fitting.
"xsize" parameter defines the number of bins extracted from the file to be used in the model.
xoff ![]() 0 parameters defines the center of the array and
it should be left at 0 in CIAO 3.2 version of the model.
0 parameters defines the center of the array and
it should be left at 0 in CIAO 3.2 version of the model.
"norm" parameter is thawed by definition and it is defined as a total number of counts (values) in the model. The best-fit value for a point-like source will be approximately equal to the number of detected counts from the source.
"xpos" parameter indicates where the center of the sub-array is located in the extracted model array, for example it should be set to the location of the source centroid if the input file is a gaussian function. Note that the initial value of the xpos is estimated using the input dataset.
| Number | Name | Description |
|---|---|---|
| 1 | file | input file name (FITS or ASCII) |
| 2 | xsize | x-full-width of the subset region of the model file |
| 3 | xoff | x-direction offset |
| 4 | xpos | x-position of the centroid in the data coordinates |
| 5 | norm | normalization |
Examples:
The example below shows the initial parameter values for the PTSRC1D model. Note that the default xsize value is set to 32 before the data file is read in. After reading the data file the xsize is set to the size of the array in the model file.
sherpa> ptsrc1d[p1]
sherpa> show p1
ptsrc1d[p1] (integrate: on)
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 file string: "none"
2 xsize frozen 32 1 1024
3 xoff frozen 0 -512 512
4 xpos thawed 12.5 12.5 197.5
5 norm thawed 1 0 1000
shrpa> p1.file="model.dat"
sherpa> show p1
ptsrc1d[p1] (integrate: on)
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 file string: "model.dat"
2 xsize frozen 38 1 38
3 xoff frozen 0 -19 19
4 xpos thawed 12.5 12.5 197.5
5 norm thawed 1 0 1000
sherpa> source 1 = p1
sherpa> fit
A 2-D file-based point-source fitting model.
PTSRC is a file-based model that may be used in fitting image data, to determine, e.g., if they are point-like or extended.
This model cannot be used as an instrument model.
FITS formats are allowed for the input model file. The current implementation requires that the image bins of the data and the PTSRC2D model file are the same.
Assume that the PSF is provided in a FITS image (file) of
size
![]() .
. ![]() and
and ![]() may be much
larger than the PSF size in pixels. An optimally sized sub-image of
size
may be much
larger than the PSF size in pixels. An optimally sized sub-image of
size
![]() can speed up
the computation of model amplitudes.
can speed up
the computation of model amplitudes.
If xoff ![]() yoff
yoff ![]() 0, the sub-image is extracted
from the center of the original image contained in file. The user may
find that changing xoff and/or yoff can
result in his or her being able to extract a smaller optimally sized
sub-image if, say, the PSF is too asymmetric to be fit easily into a
centered rectangle.
0, the sub-image is extracted
from the center of the original image contained in file. The user may
find that changing xoff and/or yoff can
result in his or her being able to extract a smaller optimally sized
sub-image if, say, the PSF is too asymmetric to be fit easily into a
centered rectangle.
If norm is thawed its best-fit value for a point-like source will be approximately equal to the number of detected counts from the source.
The parameters xpos and ypos indicate where the center of the sub-image is to be placed in the data image that is to be analyzed, i.e., they should be set to the location of the source centroid. Note that the initial values of the xpos and ypos are estimated using the input dataset.
| Number | Name | Description |
|---|---|---|
| 1 | file | input FITS file name |
| 2 | xsize | x-width of the subset region of kernel file to use in convolution |
| 3 | ysize | y-width of the subset region of kernel file to use in convolution |
| 4 | xoff | x-direction offset |
| 5 | yoff | y-direction offset |
| 6 | xpos | x-position of the centroid in data image coordinates |
| 7 | ypos | y-position of the centroid in data image coordinates |
| 8 | norm | normalization defined as a sum over the model image |
Examples:
The example below shows the initial parameter values for the PTSRC2D model. Note that the default xsize and ysize values are set to 32. After reading the data file these parameter can be adjusted to expand the image and include most of the PSF fraction. Notice after image command indicates the fraction of PSF included in the sub-image.
sherpa> ptsrc2d[p2]
sherpa> show p2
ptsrc2d[p2] (integrate: on)
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 file string: "none"
2 xsize frozen 32 1 1024
3 ysize frozen 32 1 1024
4 xoff frozen 0 -512 512
5 yoff frozen 0 -512 512
6 xpos thawed 128.5 0.5 256.5
7 ypos thawed 128.5 0.5 256.5
8 norm thawed 1 0 1000
sherpa> p2.file=psf2.fits
sherpa> show p2
ptsrc2d[p2] (integrate: on)
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 file string: "psf2.fits"
2 xsize frozen 32 1 1024
3 ysize frozen 32 1 1024
4 xoff frozen 0 -512 512
5 yoff frozen 0 -512 512
6 xpos thawed 128.5 0.5 256.5
7 ypos thawed 128.5 0.5 256.5
8 norm thawed 1 0 1000
sherpa> image p2
NOTE: PSF fraction for (xsize,ysize): FRAC = 0.984733
sherpa> p2.xsize=64
sherpa> p2.ysize=64
sherpa> image p2
Another name for the HUBBLE model. See Section 5.33.
A 1-D instrument model.
RSP is used to model instrument response. It has two parameters (as listed below): ARF and RMF filenames. The ARF file contains an ancillary response vector representing effective area as a function of photon energy, while the RMF file contains the redistribution matrix which maps photon energy to, e.g., PHA bin.
There are several things to be aware of:
See the documentation on the INSTRUMENT command. See also the FARF1D and FRMF1D instrument models.
| Number | Name | Description |
|---|---|---|
| 1 | rmf | RMF file name |
| 2 | arf | ARF file name |
A 2-D instrument model utilizing an exposure map and point-spread function.
RSP2D is used to model instrument response with an exposure map and point-spread function (PSF).
Note the following:
See the documentation on the INSTRUMENT command. See also the FARF2D and FPSF2D instrument models, for a fuller explanation of the parameters.
| Number | Name | Description |
|---|---|---|
| 1 | psffile | PSF file name |
| 2 | xsize | x-full-width of the subset region of the PSF file to use in convolution |
| 3 | ysize | y-full-width of the subset region of the PSF file to use in convolution |
| 4 | xoff | x-direction offset |
| 5 | yoff | y-direction offset |
| 6 | fft | convolution type: 1 |
| 7 | empfile | exposure map file name |
Schechter function. Integration OFF.
An integrated 1-D Schechter model:
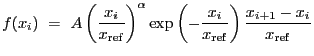 |
(5.71) |
| Number | Name | Description |
|---|---|---|
| 1 | alpha | power coefficient |
| 2 | ref | reference value
|
| 3 | norm | normalization factor |
Exponential function, base 10. Integration OFF.
An exponential model, base 10:
| (5.72) |
| Number | Name | Description |
|---|---|---|
| 1 | offset | offset
|
| 2 | coeff | coefficient |
| 3 | ampl | amplitude |
Exponential function. Integration OFF.
An exponential model:
| (5.73) |
| Number | Name | Description |
|---|---|---|
| 1 | offset | offset x_off |
| 2 | coeff | coefficient C |
| 3 | ampl | amplitude A |
Logarithm function, base 10. Integration OFF.
A base-10 logarithm model:
| (5.74) |
| Number | Name | Description |
|---|---|---|
| 1 | offset | offset
|
| 2 | coeff | coefficient |
| 3 | ampl | amplitude |
Natural logarithm function. Integration OFF.
A natural logarithm model:
| (5.75) |
| Number | Name | Description |
|---|---|---|
| 1 | offset | offset
|
| 2 | coeff | coefficient |
| 3 | ampl | amplitude |
Sine function. Integration OFF.
A 1-D sine model:
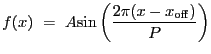 |
(5.76) |
| Number | Name | Description |
|---|---|---|
| 1 | period | period |
| 2 | offset | x offset
|
| 3 | ampl | amplitude |
Square root function. Integration OFF.
A 1-D square-root model:
| (5.77) |
| Number | Name | Description |
|---|---|---|
| 1 | offset | offset
|
| 2 | ampl | amplitude |
Another name for the HIGHPASS model. See Section 5.32.
Another name for the LOWPASS model. See Section 5.40.
Tangent function. Integration OFF.
A 1-D tangent model:
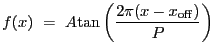 |
(5.78) |
| Number | Name | Description |
|---|---|---|
| 1 | period | period |
| 2 | offset | x offset
|
| 3 | ampl | amplitude |
A 1-D TCD-model-based instrument model.
TPSF1D is a model-based instrument model. It utilizes the predefined Gaussian, box, and top hat functions of the TCD library.
Note that Top Hat function cannot be used in version 3.2
The convolution can be performed using either Fast Fourier Transforms
(FFTs, the default), or the sliding cell technique (see the parameter
fft). If the axis length is ![]() and
the length of the kernel axis is
and
the length of the kernel axis is
![]() , then the computation time for the
sliding cell goes as
, then the computation time for the
sliding cell goes as
![]() , i.e. for
large kernels the best choice is using the FFT. A rough rule-of-thumb
for 1-D fits is to use the FFT if
, i.e. for
large kernels the best choice is using the FFT. A rough rule-of-thumb
for 1-D fits is to use the FFT if ![]() .
.
In Sherpa version 3.0.2, a new parameter is introduced: radial. If set to 1 the kernel array will be extended and its values reflected across the edge boundary. The resultant function will be symmetric. The default value (set to 0) should be used in version 3.2.
See the documentation on the INSTRUMENT command.
| Number | Name | Description |
|---|---|---|
| 1 | xsize | x-axis kernel width (pixels) |
| 2 | nsigma | sigma kernel width (Gaussian only) |
| 3 | funcTyp | Gaussian (1) / box (2) / top-hat (3) |
| 4 | fft | convolution type: 1 |
| 5 | radial | radial profile: 1 |
Examples:
This example illustrate the definition of the TPSF1D model.
sherpa> tpsf1d[t1]
sherpa> show t1
tpsf1d[t1]
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 xsize frozen 4 1 1024
2 nsigma frozen 2 1e-02 100
3funcTyp frozen 1 0 7
4 fft frozen 1 0 1
5 radial frozen 0 0 1
The Function Type is: Gaussian.
The parameter funcTyp in t1 model indicate
that the Gaussian function will be used. The 1 sigma width of the
Gaussian is set to xsize![]() 4 bins and the total size of the
Gaussian kernel is set to 2 sigma.
4 bins and the total size of the
Gaussian kernel is set to 2 sigma.
A 2-D TCD-model-based instrument model.
TPSF is a model-based 2D instrument model. It utilizes the predefined Gaussian, box, and top hat functions of the TCD library. It can represent the point-spread function (PSF), a redistribution function that maps photon spatial locations to image bins.
Note that the top hat function cannot be used in version 3.2
The convolution can be performed using either Fast Fourier Transforms
(FFTs, the default), or the sliding cell technique (see the parameter
fft). If the length of one axis is ![]() and the length of the kernel axis is
and the length of the kernel axis is
![]() , then the
computation time for the sliding cell goes as
, then the
computation time for the sliding cell goes as
![]() , i.e. for large kernels the best choice is using the
FFT. A rough rule-of-thumb for 2-D fits is to use the FFT if
, i.e. for large kernels the best choice is using the
FFT. A rough rule-of-thumb for 2-D fits is to use the FFT if
![]() .
.
See the documentation on the INSTRUMENT command.
| Number | Name | Description |
|---|---|---|
| 1 | xsize | x-axis 1 sigma width (pixels) |
| 2 | ysize | y-axis 1 sigma width (pixels) |
| 3 | nsigma | kernel width in sigma (Gaussian only) |
| 4 | funcTyp | Gaussian (1) / box (2) / top-hat (3) |
| 5 | fft | convolution type: 1 |
Examples:
This example illustrates the definition of the TPSF1D model.
sherpa> tpsf2d[t2]
sherpa> show t2
tpsf2d[t2]
Param Type Value Min Max Units
----- ---- ----- --- --- -----
1 xsize frozen 4 1 1024
2 ysize frozen 4 1 1024
3 nsigma frozen 2 1e-02 100
4funcTyp frozen 1 0 7
5 fft frozen 1 0 1
The Function Type is: Gaussian.
The parameter funcTyp in t2 model indicate
that the Gaussian function will be used. The 1 sigma width of the
Gaussian is set to xsize![]() ysize
ysize![]() 4 pixels and the total size of the
Gaussian kernel is set to 2 sigma.
4 pixels and the total size of the
Gaussian kernel is set to 2 sigma.
User implemented model.
It is possible for the user to create and implement his or her own model, own optimization method, and own statistic function within Sherpa. The User Models, Statistics, and Methods Within Sherpa chapter of the Sherpa Reference Manual has more information on this topic.
The tar file sherpa_user.tar.gz contains the files needed to define the usermethod, e.g Makefiles and Implementation files, plus example files, and it is available from the Sherpa threads page: Data for Sherpa Threads
XSpec model functions.
Sherpa includes the "additive" and "multiplicative" models of XSpec version 11.3. To use these models, simply prefix the original XSpec name by "xs"; for example, the name xsphabs represents the XSpec phabs model. To define a composite XSpec model such as
| (5.79) |
sherpa> xsphabs[abs1] sherpa> xsapec[gas1] sherpa> source 1 = abs1 * gas1
(Of course, one can use names other than "abs1" and "gas1" to represent these model components.)
Note that XSPEC models are always integrated over a bin and so require binned data.
These models also expect that the x-values will always be energy bins. When the analysis setting is using non-energy bins (e.g., ANALYSIS WAVE) and an XSPEC model is defined, Sherpa converts the bins to energy before sending them to the XSPEC model. After the XSPEC model finishes, Sherpa converts back to the original units. Sherpa also scales the model values appropriately (e.g., if counts/keV came out of the XSPEC model, and Sherpa is working with wavelength bins, then Sherpa scales the output of the XSPEC model to counts/Angstrom).
The following XSPEC components are NOT included in CIAO 3.4:
The available XSpec models are listed below. Please see either the ahelp page for each model (e.g. "ahelp xsabsori") or the XSpec User's Guide for more information about each of these models. Note that the ahelp files describe the version of the XSpec model included in CIAO, while the XSpec User's Guide may reference a newer version with different options.
| Description | |
| absori | Ionized absorber |
| acisabs | Decay in the ACIS quantum efficiency |
| apec | APEC thermal plasma model |
| bapec | APEC thermal plasma model with velocity broadening as a free parameter |
| bbody | Blackbody spectrum |
| bbodyrad | Blackbody spectrum with norm proportional to surface area |
| bexrav | E-folded broken power law reflected from neutral matter |
| bexriv | E-folded broken power law reflected from ionized matter |
| bknpower | Broken power law |
| bmc | Comptonization by relativistically moving matter |
| bremss | Thermal bremsstrahlung |
| bvapec | APEC thermal plasma model with variable abundances and velocity broadening as a free parameter |
| c6mekl | 6th-order Chebyshev polynomial DEM using mekal |
| c6pmekl | Exponential of 6th-order Chebyshev polynomial DEM using mekal |
| c6pvmkl | Variable abundance version of c6pmekl |
| c6vmekl | Variable abundance version of c6mekl |
| cabs | Compton scattering (non-relativistic) |
| cemekl | Multi-temperature mekal |
| cevmkl | Multi-temperature vmeka |
| cflow | Cooling flow model |
| compbb | Comptonized blackbody spectrum after Nishimura et al. (1986) |
| compls | Comptonization spectrum after Lamb and Sanford (1979) |
| compst | Comptonization spectrum after Sunyaev and Titarchuk (1980) |
| comptt | Comptonization spectrum after Titarchuk (1994) |
| constant | Energy-independent multiplicative factor |
| cutoffpl | Power law with high energy exponential cutoff |
| cyclabs | Cyclotron absorption line |
| disk | Disk model |
| diskbb | Multiple blackbody disk model |
| diskline | Line emission from relativistic accretion disk |
| diskm | Disk model with gas pressure viscosity |
| disko | Modified blackbody disk model |
| diskpn | Accretion disk around a black hole |
| dust | Dust scattering out of the beam |
| edge | Absorption edge |
| equil | Equilibrium ionization collisional plasma model from Borkowski |
| expabs | Low-energy exponential cutoff |
| expdec | Exponential decay |
| expfac | Exponential factor |
| gabs | Multiplicative gaussian absorption line |
| gaussian | Simple gaussian line profile |
| gnei | Generalized single ionization NEI plasma model |
| grad | GR accretion disk around a black hole |
| grbm | Gamma-ray burst model |
| highecut | High energy cutoff |
| hrefl | Simple reflection model good up to 15 keV |
| laor | Line from accretion disk around a black hole |
| lorentz | Lorentzian line profile |
| meka | Mewe-Gronenschild-Kaastra thermal plasma (1992) |
| mekal | Mewe-Kaastra-Liedahl thermal plasma (1995) |
| mkcflow | Cooling flow model based on mekal |
| nei | Simple nonequilibrium ionization plasma model |
| notch | Notch line absorption |
| npshock | Plane-parallel shock with ion and electron temperatures |
| nsa | Spectra in the X-ray range (0.05-10 keV) emitted from a hydrogen atmosphere of a neutron star. |
| nteea | Pair plasma model |
| pcfabs | Partial covering fraction absorption |
| pegpwrlw | Power law with pegged normalization |
| pexrav | Exponentially cutoff power law reflected from neutral matter |
| pexriv | Exponentially cutoff power law reflected from ionized matter |
| phabs | Photo-electric absorption |
| plabs | Absorption model with power law dependence on energy |
| plcabs | Cutoff power law observed through dense, cold matter |
| posm | Positronium continuum |
| powerlaw | Simple photon power law |
| pshock | Constant temperature, plane-parallel shock plasma model |
| pwab | Extension of partial covering fraction absorption into a power-law distribution of covering fraction |
| raymond | Raymond-Smith thermal plasma |
| redden | IR/optical/UV extinction from Cardelli et al. (1989) |
| redge | Recombination edge |
| refsch | E-folded power law reflected from an ionized relativistic disk |
| sedov | Sedov model with electron and ion temperatures |
| smedge | Smoothed absorption edge |
| spline | Spline multiplicative factor |
| srcut | Synchrotron radiation from cutoff electron distribution |
| sresc | Synchrotron radiation from escape-limited electron distribution |
| SSS_ice | Einstein Observatory SSS ice absorption |
| step | Step function convolved with gaussian |
| TBabs | Calculates the absorption of X-rays by the ISM |
| TBgrain | Calculates the absorption of X-rays by the ISM with variable hydrogen to H2 ratio and grain parameters |
| TBvarabs | Calculates the absorption of X-rays by the ISM, allowing user to vary all abundances, depletion factors, and grain properties |
| uvred | UV reddening |
| vapec | APEC thermal plasma model with variable abundances |
| varabs | Photoelectric absorption with variable abundances |
| vbremss | Thermal bremsstrahlung spectrum with variable H/He |
| vequil | Ionization equilibrium collisional plasma model with variable abundances |
| vgnei | Non-equilibrium ionization collisional plasma model with variable abundances |
| vmcflow | Cooling flow model based on vmekal |
| vmeka | M-G-K thermal plasma with variable abundances |
| vmekal | M-K-L thermal plasma with variable abundances |
| vnei | Non-equilibrium ionization collisional plasma model with variable abundances |
| vnpshock | Plane-parallel shock plasma model with separate ion and electron temperatures and variable abundances |
| vphabs | Photoelectric absorption with variable abundances |
| vpshock | Constant temperature, plane-parallel shock plasma model with variable abundances |
| vraymond | Raymond-Smith thermal plasma with variable abundances |
| vsedov | Sedov model with separate ion and electron temperatures and variable abundances |
| wabs | Photoelectric absorption (Morrison and McCammon) |
| wndabs | Photoelectric absorption with low energy window |
| xion | Reflected spectra of a photo-ionized accretion disk or ring |
| zbbody | Redshifted blackbody |
| zbremss | Redshifted thermal bremsstrahlung |
| zedge | Redshifted absorption edge |
| zgauss | Redshifted gaussian |
| zhighect | Redshifted high energy cutoff |
| zpcfabs | Redshifted partial covering absorption |
| zphabs | Redshifted photoelectric absorption |
| zpowerlw | Redshifted power law |
| zTBabs | Calculates the absorption of X-rays by the ISM for modeling redshifted absorption. Does not include a dust component. |
| zvarabs | Redshifted photoelectric absorption with variable abundances |
| zvfeabs | Redshifted absorption with variable iron abundance |
| zvphabs | Redshifted photoelectric absorption with variable abundances |
| zwabs | Redshifted "Wisconsin absorption'' |
| zwndabs | Redshifted photoelectric absorption with low energy window |
cxchelp@head.cfa.harvard.edu