HETGS and the Crab

This simulation is intended to support the in-flight calibration of the Chandra HETGS. This target has been observed by many other X-ray telescopes and has been used as an absolute calibrator many times because the source is bright, has a well-determined continuum spectrum, and is not significantly variable (excluding pulsations). Two different observations will be performed where the ACIS-S CCDs will be operated in two different clocking modes:

*TE -This is the normal operating mode of the ACIS detectors, where events are collected in 3.2 s exposures. Full imaging information is available. A 10 ks observation in this mode is used for verifying the absolute effective area of the HETGS. Simulation for this one is in progress and not shown here.

*CC - Events are continuously clocked along the columns so that position information along the columns is lost but events are timed to a relative accuracy of 3 ms. A 2 ks observation in this mode will help verify the absolute and relative timing accuracy of CC mode observations because the Crab pulsar is bright and has a well known pulse phase and period.

Simulation Setup

The source model consists of a nebula image, based on Einstein HRI observations, and a point source at the location of the pulsar. The original HRI image also contained the pulsar, of course, so the image was modelled using a 2D polynomial surface fitted to all the nebula data and excluding the pulsar region. The resultant image still has a bit of ``ringing'' due to the low order of the fitting functions. Figure 9 shows the image of the nebula by itself.

**Figure 9:** Image of the Crab nebula without the pulsar
$\begin{figure}\centering \resizebox{\textwidth}{!}{\includegraphics{marshallfig1.ps}}\end{figure}$

The spectrum of the nebula was assumed to be a simple power law with photon index 2.05 and a normalization of 10 ph/cm²/s/keV (at 1 keV) which is absorbed by a neutral intervening gas with cosmic abundances and an equivalent hydrogen column density of 3 $\times$ 10²¹ atoms/ cm². The exposure time was 10,000 s. The nebula and the pulsar were simulated separately using MARX and then combined using the marxcat routine supplied in the MARX distribution (available from the Chandra X-ray Center via ftp). The spectrum of the pulsar was assumed to be a simple power law with photon index of 1.73 and a normalization of 0.35 (same units), as given by Pravdo et al. (1981, Ap.J., 246, 484).

Images from the Simulation

The image of the 0th order is shown in Figure 10, which shows that the pulsar has been added back to the nebula. Figure 11 shows the full ACIS-S image with the HETGS dispersion creating crossing bands that are broadened due to the angular size of the nebula. The images were produced using the marx2fits program supplied with the MARX distribution.

**Figure 10:** The Crab nebula and pulsar image of the HETGS 0th order from the simulation.
$\begin{figure}\centering \resizebox{\textwidth}{!}{\includegraphics{marshallfig2.ps}}\end{figure}$

**Figure 11:** The full image of the HETGS Crab nebula simulated observation. All 6 CCDs are shown. The narrow streaks that cross near the point in the center are the dispersed spectra of the pulsar; HEG going from upper left down to the lower right while the MEG runs from lower left to upper right. There are wave-like artifacts in the image of the nebula due to the fitting method in which the nebula was isolated from the pulsar point source. The nebula produces a spectrum in the HEG and MEG separately as well, giving the pulsar spectrum a bright ``background''
$\begin{figure}\centering \resizebox{\textwidth}{!}{\includegraphics{marshallfig3.ps}}\end{figure}$

Analysis Results

Absolute Timing

One of the observations of the Crab pulsar will be done in order to check the absolute and internal timing of events from the ACIS detectors. The photon list was processed as though the ACIS-S CCDs were operated in the ``continuous clocking'' mode. The simulation and analysis steps were combined into one IDL script. There were several steps required to add suitable timing information to the event data:

1 A pulse profile was derived from previous HRI observations (Harnden & Seward 1984, Ap.J., 283, 279).

3 The event pulse phases are computed and then randomly assigned values according to the integral of the pulse profile from step 1 using the IDL procedure rephase.

4 Event times are shifted according to CCD number because the CCD parallel shifts are not started simultaneously.

5 A delay is added to each time according to its distance along the column from the readout row.

6 Event times are truncated to integer increments of 3 ms to emulate the loss of information about when the event occured within a row.

After these steps defined the ``simulation'', the events were ``analyzed'' by trying to reverse the timing offsets using only ``observed'' event values: x, f, E, D where x is the event column, f is the frame time (an integer number of 0.003 s intervals), E is the energy of the event based on the ACIS pulse height, and D is the CCD ID number (4-9). The analysis steps consisted of:

1 Forming a ``real'' clock time, c, by adding a random timing offset between 0 and 0.003 s to the frame time.

2 Finding the x position of 0th order, x0, by fitting a Gaussian to ahistogram near the expected x location.

3 Estimating wavelengths from x-x0 using both the MEG and HEG dispersion relations, as projected along x.

4 Assigning events to MEG or HEG when $\vert( hc/\lambda_{M,H} - E )\vert < dE$ , where dE is 150 eV (hc = 12.399/A/keV).

5 Computing the difference between the projected row location (given the MEG or HEG arm) and the reference y location (y0) where the pulsar should be (from aspect) and then correcting times by 3 ms for each row.

7 Folding over the pulse period after setting the reference time to the offset when 0th order is clocked out based on y0.

Upon folding, the expected and observed pulse profiles were plotted for both the MEG and HEG photons. Errors in the MEG/HEG assigment (step 4 of the analysis) will result in a randomization of these events' pulse phases. Figure 12 shows the results for the MEG events only.

**Figure 12:** The Crab pulsar light curve: input data, simulated HETGS data, and recovered light curve.
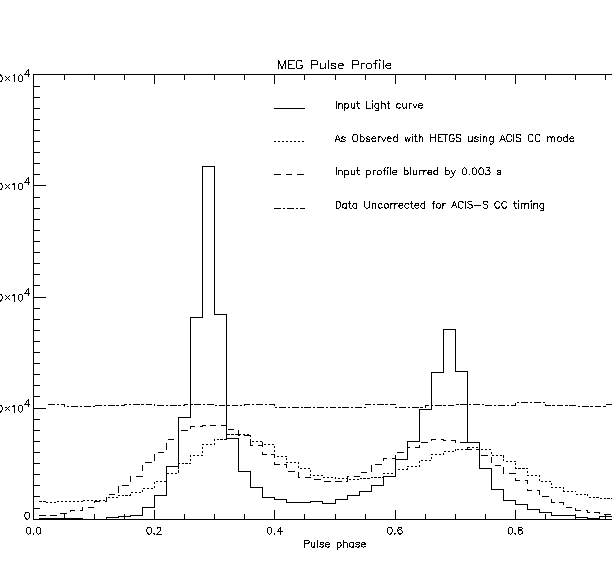$\begin{figure}\centering \resizebox{\textwidth}{!}{\includegraphics{marshallfig4.ps}}\end{figure}$

The solid line shows what the input pulse profile would be when binned to the resolution of the plot. The dash-dot line shows the histogram of (HEG & MEG) event times before any timing corrections are applied, as given in the analysis steps. The dotted line gives the event phase histogram after applying the corrections. For comparison, the dashed curve shows a simple convolution of the expected pulse profile with a Gaussian with sigma = 3 ms. Several conclusions can be drawn from the analysis of this simulation:

*The pulse profile is broadened relative to the expected profile by a Gaussian with sigma = 3 ms

*There remains a systematic offset in the pulse phase that has not been accounted for properly

*An unexpectedly large number of events appear near phase 0.0 where the input pulse profile is at a minimum

There are several effects that contribute to the blurring of the pulse profile. First is the discreteness of the ACIS readout clocking, which limits timing to 3 ms. Second is the finite size of the telescope/grating cross dispersion profile which blurs events of a given time by a vertical displacement which is then translated to a timing offset.

Further analysis of the simulation will be required to find the cause of the systematic timing offset, which appears to be about 2 ms. The zeroth order may be used to test the event timing reconstruction algorithm but will not verify steps 2-5 of the analysis.