Chandra Peers into Neutron Stars
Craig Heinke (University of Alberta)
The interiors of neutron stars contain some of the densest matter, other than black holes, in the universe, reaching at least several times the density of atomic nuclei. Observations of neutron stars thus give us the opportunity to constrain the exotic physics of how matter behaves at such incredibly high densities. In this article, I describe a few of the insights into the interior physics of neutron stars provided by the Chandra X-ray Observatory.
Introduction
Neutron stars are not uniform in density. We can divide them into four main parts: (i) an inner core at high density where the matter may be in an exotic state, (ii) an outer core, which we think is made mostly of neutrons, (iii) a crust comprised of unbound nucleons at the base layer transitioning to normal nuclei at the top layer via the intermediate “nuclear pasta” layer where nucleons assemble into complicated structures, and, (iv) a thin (mere centimeters thick!) atmosphere on the surface (Figure 1).
The simplest model for neutron star interiors is that both the inner and outer core consist principally of neutrons, with some protons, electrons, and muons. However, we do not really know what configuration matter settles into at such high densities. Particle colliders such as the Large Hadron Collider smash protons together to reach very high densities, but these high densities are reached only for very short times at high temperatures. It’s possible that matter at very high densities, allowed to settle down at relatively cold temperatures (e.g. less than billions of degrees!), may undergo a phase transition to another state. The quarks that constitute nucleons may rearrange to form other subatomic particles, such as hyperons, kaons, or pions; or the quarks could completely dissolve into “strange quark matter”. If a portion of the quarks can settle into such states in the core of a neutron star, then even higher densities may exist in the core, thus reducing the maximum mass that will trigger a collapse into a black hole. For “normal” neutron-rich matter in neutron stars, we do not know what fraction of the mass is protons and electrons; the proton fraction alters the pressure for a given density (the equation of state). Thus, measurements of the masses and radii of neutron stars can strongly constrain the physics of neutron star interiors.
Neutron star interiors are theorized to show a wide range of other fascinating physics. On Earth, lowering the temperature of either helium isotope (helium-3 or helium-4) to near absolute zero allows the helium to enter a “superfluid” liquid state, in which the particles are able to move without friction. In neutron star interiors, Migdal (1959, Nucl. Phys. 13, 655) suggested that the neutrons and protons can enter superfluid states, at (relatively) “low” temperatures, of order a billion degrees! Since the protons are charged, their superfluidity also implies superconductivity. The consequences of the superfluid state include quantization of the angular momentum into individual vortices, and confinement of the magnetic field into flux tubes. Glitches in pulsar spindown (temporary spin-up of the neutron star, followed by relaxation to the normal spindown path) are generally understood as indicating time-variable angular momentum transfers between vortices of neutron superfluid in the crust (not the same superfluid state as in the interior!) and the outer crust, composed of non-superfluid neutrons (Anderson & Itoh, 1975, Nature, 256, 25). Neutron stars are born at extremely high temperatures, and for their first million years cool principally via neutrino emission from their cores. The transition to a superfluid state, and the proton fraction, dramatically influence the neutrino emission, and thus thermal evolution, of neutron stars.
Most of our knowledge of neutron stars comes from radio studies of pulsars, but the radio emission arises from electrons trapped in the magnetic field lines well above the surface, giving limited information about the neutron star interior. X-ray observations give direct access to emission from the neutron star surface, which is useful for constraining the interior physics. Chandra’s unparalleled angular resolution, high sensitivity, and excellent spectral resolution have enabled several key discoveries.
Mass and Radius
Accurately determining the mass and radius for even one neutron star (or better yet, several) would significantly constrain the possible compositions of neutron star cores, and the equation of state. Radio pulsar timing observations have been able to measure highly precise masses, often using a distinctive feature in the arrival times of radio pulses caused by the general relativistic delay of light as it passes a massive object (e.g. the companion star), Shapiro delay (Shapiro, 1964, PRL 13, 789). Such observations have measured precise masses of a significant number of pulsars, including two pulsars with masses close to 2.0 solar masses (Demorest et al. 2010, Nature, 467, 1081; Antoniadis et al. 2013, Science, 340, 448; Ozel & Freire 2016, ARA&A, 54, 401).
Radius measurements, on the other hand, have been harder, though there are several avenues to constrain neutron star radii. Neutron stars spinning too fast will break up, so the maximum observed pulsar spin rate, 716 Hz (Hessels et al. 2006, Science, 311, 1901), limits the radius of this neutron star to below 14.3 km (assuming a typical neutron star mass of 1.4 Msun). The simplest method, conceptually, is to measure the X-ray flux and temperature of the hot neutron star surface. Assuming blackbody emission without relativistic effects, we can then infer the angular size of the neutron star, and, if the distance is known, its radius. However, general relativistic redshifting of the spectrum induces a degeneracy between mass and radius, so we actually measure the apparent radiation radius, R∞=R (1-2GM/(Rc2))-½. Furthermore, the spectrum of light from a neutron star is not a blackbody, but is determined by the passage of light through the thin neutron star atmosphere, which must be modeled. Finally, if the surface is not at a uniform temperature, then the measurement will only provide a lower limit on the radius.
Pulsars are heated at their poles, so do not emit uniformly, and the nature of their atmospheres is generally not certain. X-ray efforts to measure neutron star radii have focused on accreting neutron stars, when light from the hot neutron star surface dominates any light from accretion flows. Thermonuclear X-ray bursts (seconds-long burning of H and He, which can exceed the Eddington luminosity and lead to rapid expansion of the photosphere) have been one focus, principally using the Rossi X-ray Timing Explorer. The signal-to-noise of these bursts is high, giving interesting constraints on the NS radius (on the order 11-13 km, e.g., Nattila et al. 2016, A&A 591, A25). The difficulty is systematic effects; principally, the exact composition of the photosphere is not easy to pin down (e.g. Nattila et al. 2017, A&A, 608, A31; Suleimanov et al. 2018, A&A, 619, A114).

Figure 2: Chandra X-ray image of the globular cluster 47 Tuc, in representative color (red 0.5-1.2 keV, green 1.2-2 keV, blue 2-6 keV). The crucial quiescent neutron star X7 is marked.
The composition of the photosphere is less of a problem when studying neutron stars between transient accretion episodes (quiescent neutron stars), as the atmosphere has time to stratify, with the lightest element (generally H) floating to the top and producing an easily modeled spectrum. Low-mass X-ray binaries where the neutron star’s magnetic field is low appear optimal for constraining the neutron star radius (Zavlin et al. 1996, A&A, 315, 141). Since globular clusters have well-known distances, and contain many quiescent neutron stars, they make ideal targets (Rutledge et al. 2002, ApJ, 578, 405), and often require Chandra’s high spatial resolution to overcome crowding. Dozens of quiescent neutron stars in globular clusters have been found with Chandra and XMM-Newton, including five in the well-studied globular cluster 47 Tucanae (Figure 2, Heinke et al. 2005, ApJ, 625, 796). Spectral fits to these objects can give stringent constraints on mass and radius, such as the neutron star X7 in 47 Tuc, where, for an assumed mass of 1.4 Msun, a radius of 11.1-0.7+0.8 km was measured (68% confidence; Bogdanov et al. 2016, ApJ, 831, 184, Figure 3).
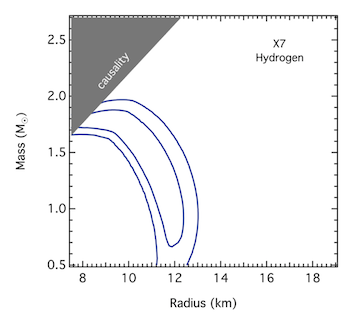
Figure 3: Constraints on the mass and radius of X7 in 47 Tuc, based on spectral fits with a hydrogen atmosphere (Bogdanov et al. 2016). The contours enclose 68% and 95% of the posterior likelihood over M and R.
Constraining the equation of state of neutron stars requires both radii and mass measurements. Since the masses of these neutron stars have not been measured (a task awaiting the Thirty-Meter Telescope!), we can only combine measurements from various sources—aided by nuclear physics—to infer constraints on the neutron star equation of state. Guillot et al. (2013, ApJ, 772, 7) pioneered a simple form for such constraints, and argued for a remarkably low neutron star radius (R=9.1+1.3-1.5 km, at 90% confidence). However, Heinke et al. (2014, MNRAS, 444, 443) argued that the quiescent neutron star in the globular cluster NGC 6397 accretes from a helium white dwarf, so the matter it accretes will lack hydrogen, and the atmosphere will be comprised of helium. A helium atmosphere leads to a harder spectrum than that of a hydrogen atmosphere. Indeed, spectral fits to a helium atmosphere allow for a larger radius, up to 13 km. Steiner et al. (2018, MNRAS, 476, 421) performed a combined analysis of the globular cluster quiescent neutron star spectra, accounting for a variety of systematic effects including different atmospheric compositions, and found a 95% confidence range of 11.0-14.3 km for the radius of a 1.4 Msun neutron star using standard assumptions of neutron star interior structure, or 10.0-11.9 km when allowing for a phase transition (Figure 4).

Figure 4: Probability distributions for radii as a function of mass, using data from 7 quiescent neutron stars, and one of two assumptions of the neutron star equation of state (left, baseline: equation of state described by polytrope; right, allowing rapid phase transitions). (Steiner et al. 2018)
Recently, LIGO/Virgo and the NICER X-ray observatory have provided strong constraints on the neutron star radius, consistent with those from Chandra studies of quiescent neutron stars. Gravitational waves from the neutron star merger GW170817 detected by LIGO/Virgo would have shown signatures of tidal deformation if the neutron stars were large enough; thus, the lack of such signatures constrains the neutron star radius to below 13.3 km at 90% confidence (Abbott et al. 2018, PRL, 121, 161101). NICER measured precise pulse profiles of X-ray pulsations from hot spots on the surface of the millisecond pulsar J0030+0451. As these pulse profiles are shaped by general relativistic (light bending) and special relativistic (beaming) effects, the NICER measurements allow tight constraints on the neutron star compactness, and constrain the radius to 12.7+1.1-1.2 km (Riley et al. 2019, ApJL, 887, L21) or 13.0+1.2-1.1 km (Miller et al. 2019, ApJL, 887, L24). Future NICER results should be even more constraining. Combining information from Chandra and XMM cluster quiescent neutron stars, RXTE bursts, LIGO/Virgo gravitational waves, and NICER pulse profiles together provides the most stringent constraints, with a preference for a radius between 11.1 and 12.8 km (95% confidence) for a 1.4 Msun neutron star (al-Mamun et al. 2021, PRL, 126, 061101), though we cannot yet judge whether neutron stars undergo strong phase transitions.
Temperature Evolution: Young Neutron Stars
The temperature evolution of hot neutron stars tells us the rate at which neutrinos are emitted from the interior of the neutron star. There are several processes by which neutrinos can be produced in neutron star cores (see, e.g., Yakovlev & Pethick 2004, ARAA, 42, 169; Page et al. 2004, ApJS, 155, 623). The simplest process is the nucleon direct Urca mechanism: when the abundance of protons becomes sufficiently high, it becomes easy for neutrons to change to protons (n → p + e− + ν) and the reverse (p + e− → n + ν). The availability of this process depends on the proton fraction, which depends on density (density should increase with the mass of the neutron star), as well as the poorly-constrained nuclear symmetry energy. Similarly, fast neutrino cooling is possible by converting protons back and forth to other particles (e.g. hyperons), or by converting to other quark varieties in a medium of strange quark matter. As both parts of the reaction produce neutrinos (or antineutrinos) which fly away unimpeded, the reaction cools the neutron star. The direct Urca mechanisms are extremely fast, and, when present, could cool neutron stars to non-detectability in X-rays within a few 100 years.
At lower proton concentrations, the direct Urca mechanism is not available, but less efficient neutrino emission processes remain available. These include the modified Urca mechanism, which requires neighboring nucleons to conserve momentum, and thus results in a slower reaction, and neutron-neutron bremsstrahlung. These two processes can dominate the cooling of hot (X-ray detectable) neutron stars.
However, the neutrino emission processes are dramatically altered when nucleon superfluidity is present (see Page et al. 2013, arXiv:1302.6626, for details). For neutrons (or protons) to enter a superfluid state requires that they pair up, producing a lower-energy paired state. Paired nucleons are unable to participate in any Urca reactions, reducing neutrino emissivity. However, around the critical temperature for the nucleons to become superfluid, pairs are repeatedly created and broken apart by thermal fluctuations. Creating a pair releases neutrinos, while breaking it absorbs thermal energy; thus, this process can effectively cool the neutron star.
We have been able to measure thermal X-rays from the surface of a number of young neutron stars. Many of these are in the centers of supernova remnants, such as the young neutron star in the Cassiopeia A supernova remnant discovered in Chandra’s first-light image (Tananbaum 1999, IAUC 7246, 1; cover image), while others are relatively young neutron stars where we estimate their age from their spin rate and the rate at which their spin is slowing down. These measurements find a range of temperatures at the same age indicating that at least one, but likely more, property is different between these neutron stars.
One possibility is that these neutron stars have different “envelopes”, the ∼100-meter layer of lower-density normal matter on the surface between the crust and atmosphere. Lighter elements like H, He, C, O have higher thermal conductivities than Fe, leading to (initially) higher temperatures, followed by a faster temperature decline at older ages, compared to iron envelopes. These neutron stars are also likely to vary in their masses, and thus central densities. The density affects the critical temperature for superfluidity, and thus the temperature range in which neutron pairs form and break, providing a fairly rapid cooling mechanism. Alternatively, should the neutron stars have access to enhanced cooling mechanisms (such as the direct Urca mechanism, or others) in part of their cores, a range of neutron star masses can also give a range of cooling rates.
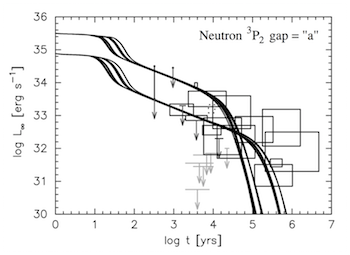
Figure 5: Luminosity vs. time for young neutron stars (boxes), compared with cooling calculations with different envelopes (the light element tracks are hotter at young ages). (D. Page et al. 2009, ApJ, 707, 1131)
Figure 5, from Page et al. 2009, compares calculations of neutron star cooling using superfluid pair forming and breaking and different neutron star envelopes, to a group of well-studied cooling neutron stars (black boxes), showing that reasonable agreement can be obtained. Interestingly, there are a number of nearby supernova remnants of reasonably well-known age without detected neutron stars despite deep Chandra or XMM observations (gray downward arrows, Kaplan et al. 2004, ApJ, 153, 269). Should those supernova remnants contain neutron stars, they must be colder than these calculations predict, likely requiring enhanced neutrino cooling mechanisms. Alternatively, these supernovae may have produced black holes.
The most direct way to study the temperature evolution of neutron stars would be to measure the actual temperature decline of a young neutron star. Heinke & Ho (2010, ApJ, 719, L167) reported a measurement of a temperature decline of the Cas A neutron star (formally a drop in flux, interpreted as a temperature decline), at the level of 3.9±0.7% over 10 years. This is so fast that it requires a transient cooling event—if it had been dropping this fast for its whole ∼340-year life, it would not be visible today. The most widely considered explanation of this cooling is that neutron superfluidity has recently turned on in the neutron star core, leading to a rapid temperature drop due to the breaking and formation of neutron pairs (Page et al. 2011, PRL, 106, 081101; Shternin et al. 2011, MNRAS, 412, L108). If so, this allows the inference of a maximal (density-dependent) critical temperature for the neutron superfluid of 0.5-1 billion K. A number of alternative scenarios for the rapid cooling have also been considered, including (i) delayed equilibrium between the crust and core due to suppressed thermal conductivity in the interior (Blaschke et al. 2012, Phys Rev C, 85, 2802), (ii) cooling after transient heating of the neutron star by dissipation of small-scale magnetic fields (Bonanno et al. 2014, A&A, 561, L5), or, (iii) the direct Urca process (to prevent too-rapid cooling, the direct Urca process must be partly suppressed by superfluidity, generally of protons; e.g. Taranto et al. 2016, MNRAS, 456, 1451).
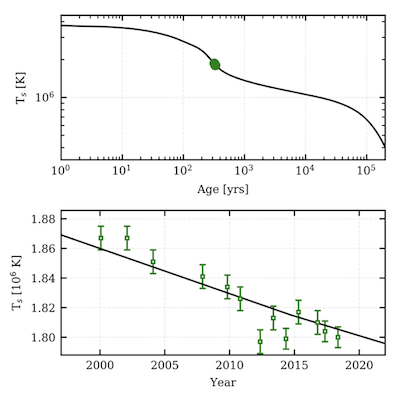
Figure 6: Top, sample temperature evolution model that matches the Cas A data. Bottom, zoom on the Cas A GRADED data with the model, showing the temperature decline. (M. Wijngaarden et al. 2019)
A number of factors complicate the temperature change measurement of the Cas A neutron star: (i) complexities caused by pileup of multiple photons, (ii) reduced sensitivity to soft photons of the ACIS detector due to increasing build-up of contaminant (at an unsteady rate), and, (iii) telemetry restrictions that limit event information (GRADED rather than FAINT mode). Telemetry restrictions arise from the high count rate of the bright supernova remnant. Measurements of the rate of temperature decline with the HRC-S instrument (Elshamouty et al. 2013, ApJ, 777, 22) and with the ACIS instrument in a subarray mode (Posselt et al. 2018, ApJ, 864, 135) mitigate some of these complications and find lower temperature declines of 1-1.6% over 10 years, but with the significance of cooling at less than 3 sigma. Recalibration of existing GRADED-mode observations, and continued observations, have reduced the inferred temperature decline to 2.2±0.2% over 10 years (Wijngaarden et al. 2019, MNRAS, 484, 974 (Figure 6); Ho et al. 2021, MNRAS, submitted). Future Chandra observations are needed to verify and improve the measurements of any temperature decline.
Temperature Evolution: Accreting Neutron Stars
An alternative method to probe the neutrino emission properties of neutron stars is to observe accreting neutron stars (generally in low-mass X-ray binaries) during (long) periods of quiescence between accretion outbursts. Neutron star cores are heated by pressure-driven fusion in the base of the crust during accretion episodes, and this heat is re-radiated during quiescent periods, on a timescale of ∼104 years (Brown, Bildsten & Rutledge 1998, ApJ, 504, L95). However, the heat may also escape the neutron star via neutrino emission from the core, via processes mentioned above. To test whether the heat is coming out as photons from the surface, or escaping via neutrinos from the core (and at what rates), requires that we measure the thermal luminosity of the neutron stars, and estimate their time-averaged accretion rates, typically by recording multiple accretion outbursts.

Figure 7: Data (points) of quiescent neutron star luminosity, compared to their time-averaged mass transfer rates. (Beznogov et al. 2015) Left: Data compared to calculated probabilities (shading), with a rapid threshold for the direct Urca process; most data points are not described well. Right: Model includes a broadened threshold for the direct Urca process (via slow introduction of proton superfluidity), allowing a range of cooling rates, which better explain the data.
Observations using Chandra and XMM of numerous low-mass X-ray binaries in quiescence have allowed us to measure their thermal surface emission and revealed surprising results. These measurements suggest that a wider range of neutrino cooling is needed when compared to young cooling neutron stars, likely even requiring enhanced cooling such as direct Urca (e.g. Colpi et al. 2001, ApJ, 548, L175; Yakovlev et al. 2003, A&A, 407, 265; Fortin et al. 2018, MNRAS, 475, 5010; Potekhin et al. 2019, A&A, 629, A88). Figure 7 (left; Beznogov & Yakovlev 2015, MNRAS, 447, 1598) illustrates that without enhanced neutrino cooling, neither the two coolest neutron stars nor the spread of neutron star cooling rates can be explained. Figure 7 (right) assumes that direct Urca neutrino cooling is available, but that it is largely suppressed by proton superfluidity in most of the stellar core; a range of neutron star masses allows for gradual suppression of proton superfluidity in the core, and thus gradual turning on of the direct Urca process. That is, low-mass neutron stars have direct Urca suppressed by proton superfluidity, but in high-mass neutron stars the densest portion of the core is not superfluid, and direct Urca processes can operate, resulting in rapid cooling. A plausible distribution of neutron star masses seems to be in accord with the cooling data in this model. Interestingly, this model requires neutron superfluidity in the core to be suppressed in most neutron stars, in tension with the most popular model used to explain the Cas A neutron star cooling.
Temperature Evolution: Physics of the Crust
Observations of X-ray binaries shortly after prolonged accretion outbursts reveal a crust that is heated out of equilibrium with the core, which will return to equilibrium on timescales of weeks to years (Rutledge et al. 2002, ApJ, 580, 413; Wijnands et al. 2017, JApA, 38, 49). The evolution of the surface temperature over time depends on the amount of heat deposited in the crust due to the outburst, and on the thermal properties (conductivity, heat capacity, etc) of the crust, with deeper layers affecting the lightcurve at later times. (Note that heating of the surface, by impact of accreted material, is radiated promptly, so later observations reveal the physics of the crust.) Chandra and XMM observations of several neutron star transients with long outbursts (Figure 8; Wijnands et al. 2017), particularly KS 1731-260 and MXB 1659-298, revealed swift cooling on timescales of a few 100 days, in some cases continuing for a decade. The rapid cooling is generally interpreted as indicating that the neutron star crust must have a high thermal conductivity—i.e., crystalline with relatively few impurities, and likely containing a neutron superfluid (Shternin et al. 2007, MNRAS, 382, L43; Brown & Cumming 2009, ApJ, 698, 1020).
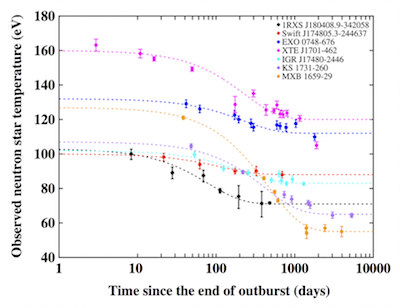
Figure 8: Temperature evolution of several neutron stars after accretion outbursts, showing the cooling of their crusts. (Wijnands et al. 2017)
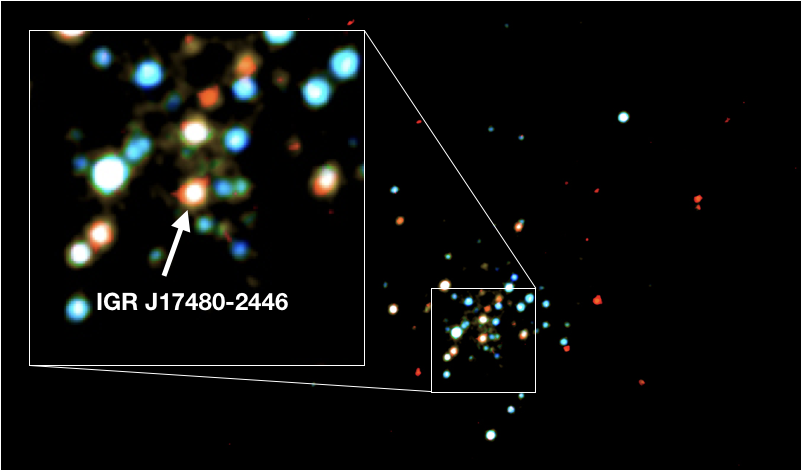
Figure 9: X-ray image of the globular cluster Terzan 5, with IGR J17480-2446 labeled. (Bahramian et al. 2020, ApJ, 901, 57)
Fascinatingly, several neutron star transients appear to be significantly hotter than expected after their observed outburst, requiring substantial extra heating of the shallow layers of the crust. Among the neutron stars needing this extra shallow heating are the two mentioned above, the 11-Hz pulsar IGR J17480-2446 in the globular cluster Terzan 5 (Degenaar et al. 2011, MNRAS, 418, L152; see Figure 9) and, especially, the neutron star transient MAXI J0556-332 (Homan et al. 2014, ApJ, 795, 131). Standard modeling of the fusion heating of the deep crust predicts ~2.0 MeV per accreted nucleon should be deposited in the deep crust during accretion. IGR J17480-2446, KS 1731-260, and MXB 1659-298 all appear to require an additional ~1.0 MeV/nucleon of shallow heating, while MAXI J0556-332 requires 6-16 MeV/nucleon of shallow heating (Deibel et al. 2015, ApJ, 809, L31). This is dramatically more than can be plausibly supplied by nuclear reactions, leading Deibel et al. to suggest that some fraction of the accretion energy (80 MeV/nucleon, expected to be radiated promptly from the surface) must be dissipated deeper in the star, perhaps by waves in a differentially-rotating envelope. The origin of this shallow heating, and other aspects of some crustal cooling curves, remain mysterious, indicating a need for further studies of sources returning to quiescence.
A particularly fascinating result comes from analysis of the accretion outbursts and cooling curves of MXB 1659-298. Brown et al. (2018, Phys Rev Letters, 120, 182701) show that, if the three observed outbursts of MXB 1659-298 are typical of this source, the heat deposited in the deep crust of MXB 1659-298 should heat the core to substantially higher than the observed temperature in quiescence (years after outbursts). To explain this, Brown et al. find that the direct Urca process should be active in at least 1% of the neutron star core (or a direct Urca-like process, e.g. involving hyperons or pions; but superfluid pair breaking and formation, or modified Urca, are not fast enough). This finding is similar to the conclusions drawn from studies of the coldest accreting neutron stars in quiescence described in the previous section, but more robust since the thermal emission is directly detected, and the cooling of the neutron star post-outburst is directly observed and modeled.
The Chandra X-ray Observatory’s abilities to measure the thermal spectra of neutron stars, at very low fluxes or in crowded environments such as supernova remnants or globular clusters, have been crucial to the discoveries highlighted in this article. Key results have included (i) crystalline structure of the outer crusts and mysterious shallow crustal heating, (ii) constraints on the neutron star radius that bring us closer to determining the equation of state, (iii) the likely transition of a stellar core into a superfluid phase, and, (iv) a larger than expected range of cooling rates among young and old neutron stars, likely requiring direct Urca (or similarly fast) cooling processes for the coldest objects. Although we have substantial data constraining the density and thermal evolution of neutron stars, we still face many puzzles in deciphering them, requiring more theoretical work and targeted observations. I have not even mentioned the magnetic fields of neutron stars, a large and growing exciting topic in the era of fast radio bursts, but that is a topic for another article.
Bibliography
Abbott et al. 2018, PhRvL,121, 161101.
Al-Mamun et al. 2021, PhRvL,126, 061101.
Anderson and Itoh 1975, Natur,256, 25.
Antoniadis et al. 2013, Sci,340, 448.
Bahramian et al. 2020, ApJ,901, 57.
Beznogov and Yakovlev 2015, MNRAS,447, 1598.
Blaschke et al. 2012, PhRvC,85, 022802.
Bogdanov et al. 2016, ApJ,831, 184.
Bonanno et al. 2014, A&A,561, L5.
Brown, Bildsten, and Rutledge 1998, ApJL,504, L95.
Brown and Cumming 2009, ApJ,698, 1020.
Brown et al. 2018, PhRvL,120, 182701.
Colpi et al. 2001, ApJL,548, L175.
Degenaar, Brown, and Wijnands 2011, MNRAS,418, L152.
Deibel et al. 2015, ApJL,809, L31.
Demorest et al. 2010, Natur,467, 1081.
Elshamouty et al. 2013, ApJ,777, 22.
Fortin et al. 2018, MNRAS,475, 5010.
Guillot et al. 2013, ApJ,772, 7.
Heinke et al. 2014, MNRAS,444, 443.
Heinke et al. 2005, ApJ,625, 796.
Heinke and Ho 2010, ApJL,719, L167.
Hessels et al. 2006, Sci,311, 1901.
Homan et al. 2014, ApJ,795, 131.
Kaplan et al. 2004, ApJS,153, 269.
Migdal 1959, Nucl. Phys. 13, 655.
Miller et al. 2019, ApJL,887, L24.
Nättilä et al. 2016, A&A,591, A25.
Nättilä et al. 2017, A&A,608, A31.
Page et al. 2011, PhRvL,106, 081101.
Page et al. 2013, arXiv, arXiv:1302.6626.
Page et al. 2004, ApJS,155, 623.
Posselt and Pavlov 2018, ApJ,864, 135.
Potekhin, Chugunov, and Chabrier 2019, A&A,629, A88.
Riley et al. 2019, ApJL,887, L21.
Rutledge et al. 2002, ApJ,580, 413.
Rutledge et al. 2002, ApJ,578, 405.
Shapiro 1964, PhRvL,13, 789.
Shternin et al. 2007, MNRAS,382, L43.
Shternin et al. 2011, MNRAS,412, L108.
Steiner et al. 2018, MNRAS,476, 421.
Suleimanov, Poutanen, and Werner 2018, A&A,619, A114.
Tananbaum 1999, IAUC,7246, 1.
Taranto, Burgio, and Schulze 2016, MNRAS,456, 1451.
Wijnands, Degenaar, and Page 2017, JApA,38, 49.
Wijngaarden et al. 2019, MNRAS,484, 974.
Yakovlev and Pethick 2004, ARA&A,42, 169.
Yakovlev, Levenfish, and Haensel 2003, A&A,407, 265.
Zavlin, Pavlov, and Shibanov 1996, A&A,315, 141.
Özel and Freire 2016, ARA&A,54, 401.

