ronment complete with fast
array-based mathematical capabilities rivaling commercial
packages such as MatLab or IDL.
Custom user models may be loaded into ISIS as either scripts
or compiled code1, without any recompilation of ISIS itself; because of the fast array manipulation native to S-Lang, scripted models suffer no needless performance penalties, while the SLIRP code generator (Noble 2003) can render the use of compiled C, C++, and FORTRAN models a nearly instantaneous, turnkey process.
Parallel Modeling
Using the PVM module we’ve parallelized a number of the numerical modeling tasks in which astronomers engage daily, and summarize them here as a series of case studies. Many of the scientific results stemming from these efforts are already appearing elsewhere in the literature.
Kerr Disk Line
Relativistic Kerr disk models are computationally expensive. Historically, implementors have opted to use precomputed tables to gain speed at the expense of limiting flexibility in searching parameter space. However, by recognizing that contributions from individual radii may be computed independently we’ve parallelized the model to avoid this tradeoff. To gauge the performance benefits2 we tested the sequential execution of a single model evaluation, using a small, faked test dataset, on our fastest CPU (a 2Ghz AMD Opteron), yielding a median runtime of 33.86 seconds. Farming the same computation out to 14 CPUs on our network reduced the median runtime to 8.16s, yielding a speedup of 4.15. While 30% efficiency seems unimpressive at first glance, this result actually represents 67% of the peak speedup of 6.16 predicted by Amdahl’s Law (5.5 of the 33.86 seconds runtime on 1 CPU was not parallelizable in the current implementation), on CPUs of mixed speeds and during normal working hours. Reducing the model evaluation time to 8 seconds brings it into the realm of interactive use, with the result that fits requiring 3-4 hours to converge (on “real” datasets such as the long XMM-Newton observation of MCG--6-30-15 by Fabian) may now be done in less than 1 hour. The model evaluation is initiated in ISIS through the S-Lang hook function
Custom user models may be loaded into ISIS as either scripts
or compiled code1, without any recompilation of ISIS itself; because of the fast array manipulation native to S-Lang, scripted models suffer no needless performance penalties, while the SLIRP code generator (Noble 2003) can render the use of compiled C, C++, and FORTRAN models a nearly instantaneous, turnkey process.
Parallel Modeling
Using the PVM module we’ve parallelized a number of the numerical modeling tasks in which astronomers engage daily, and summarize them here as a series of case studies. Many of the scientific results stemming from these efforts are already appearing elsewhere in the literature.
Kerr Disk Line
Relativistic Kerr disk models are computationally expensive. Historically, implementors have opted to use precomputed tables to gain speed at the expense of limiting flexibility in searching parameter space. However, by recognizing that contributions from individual radii may be computed independently we’ve parallelized the model to avoid this tradeoff. To gauge the performance benefits2 we tested the sequential execution of a single model evaluation, using a small, faked test dataset, on our fastest CPU (a 2Ghz AMD Opteron), yielding a median runtime of 33.86 seconds. Farming the same computation out to 14 CPUs on our network reduced the median runtime to 8.16s, yielding a speedup of 4.15. While 30% efficiency seems unimpressive at first glance, this result actually represents 67% of the peak speedup of 6.16 predicted by Amdahl’s Law (5.5 of the 33.86 seconds runtime on 1 CPU was not parallelizable in the current implementation), on CPUs of mixed speeds and during normal working hours. Reducing the model evaluation time to 8 seconds brings it into the realm of interactive use, with the result that fits requiring 3-4 hours to converge (on “real” datasets such as the long XMM-Newton observation of MCG--6-30-15 by Fabian) may now be done in less than 1 hour. The model evaluation is initiated in ISIS through the S-Lang hook function
public define pkerr_fit (lo, hi, par)
{
variable klo, khi;
(klo, khi) = _A(lo, hi); % convert angstroms to KeV
return par[0] * reverse ( master (klo, khi, par));
}
where lo and hi are arrays (of roughly 800
elements) representing the left and right edges of each bin
within the model grid, and par is a 10 element array of the Kerr
model parameters. Use of the PVM module is hidden within
the master call (which partitions the disk
radii computation into slave tasks), allowing ISIS to remain
unaware that the model has even been parallelized. This is
an important point: parallel models are installed and
later invoked using precisely the same mechanisms employed
for sequential models.
For each task the slaves invoke a FORTRAN kerr model implementation, by Laura Breneman at the University of Maryland, wrapped by SLIRP as follows:
linux% slirp -make kerr.f
Starter make file generated to kerr.mf
linux% make -f kerr.mf
Confidence Contours and Error Bars
Error analysis is ripe for exploitation with parallel methods. In the 1D case, an independent search of χ2 space may be made for each of the I model parameters, using N=I slaves, with each treating one parameter as thawed and I-1 as fixed. Note that superlinear speedups are possible here, since a slave finding a lower χ2 value can immediately terminate its N-1 brethren and restart them with updated parameters values. Parallelism in the 2D case is achieved by a straightforward partition of the parameter value grid into J independently-evaluated rectangles, where J >> N (again, the number of slaves) is typical on our cluster. Our group and collaborators have already published several results utilizing this technique. For example, Allen et al 2004 describes joint X-ray, radio, and γ-ray fits of SN1006, containing a synchrotron radiation component modeled as
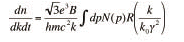
This also makes it easy for ISIS to employ an MPI module for parallelism, if desired.
For each task the slaves invoke a FORTRAN kerr model implementation, by Laura Breneman at the University of Maryland, wrapped by SLIRP as follows:
linux% slirp -make kerr.f
Starter make file generated to kerr.mf
linux% make -f kerr.mf
Confidence Contours and Error Bars
Error analysis is ripe for exploitation with parallel methods. In the 1D case, an independent search of χ2 space may be made for each of the I model parameters, using N=I slaves, with each treating one parameter as thawed and I-1 as fixed. Note that superlinear speedups are possible here, since a slave finding a lower χ2 value can immediately terminate its N-1 brethren and restart them with updated parameters values. Parallelism in the 2D case is achieved by a straightforward partition of the parameter value grid into J independently-evaluated rectangles, where J >> N (again, the number of slaves) is typical on our cluster. Our group and collaborators have already published several results utilizing this technique. For example, Allen et al 2004 describes joint X-ray, radio, and γ-ray fits of SN1006, containing a synchrotron radiation component modeled as
This also makes it easy for ISIS to employ an MPI module for parallelism, if desired.