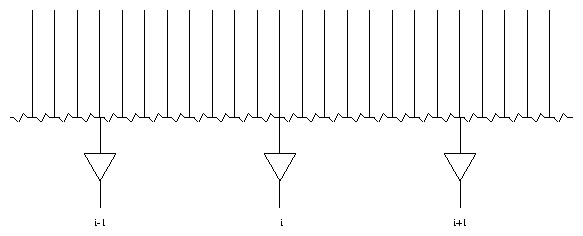
The HRC uses a crossed grid charge detection scheme to register the position of the charge cloud produced by an event emerging from the bottom of the MCP stack[1]. This method was used for the Einstein and ROSAT HRIs. A detailed explanation of the operating principle of the crossed grid charge detector (CGCD) can be found in Chappell & Murray (1989)[2]. Briefly, the HRC CGCD consists of two planes of ``wires'' that run perpendicular to each other. As shown in figure 1, adjacent wires along a single axis are connected via resistors and every eighth wire is connected to a charge amplifier.

The charge that is deposited on an individual wire is divided between the two nearest charge amps in inverse proportion to the ratio of resistances from the wire to the amps. Using the signals from the three amplifiers centered on the charge cloud, the event position relative to the central amplifier can be determined via a ``three tap position algorithm''[2]:
|
The event coarse position is determined by the HRC instrument by the following process (all accomplished using analog and digital hardware components): An event is detected when the signal from the back MCP exceeds a commandable threshold value. Once the event is detected the signals from the taps on the CGCD are sampled and compared to a threshold. A set of ``UP'' and ``DOWN'' priority encoders are used to determine the lowest and highest tap numbers for which the signals exceeded the threshold. These two numbers are averaged to return a candidate coarse position (the UP encoded value is added to the inverted DOWN encoded value and divided by 2). The two taps that bracket the candidate coarse position (or the candidate and the next higher) are compared to each other to determine the higher value and that tap number becomes the actual coarse position. This tap signal and the two adjacent signals are selected for further processing. The three signals are input to amplifiers with selectable gains for which the gain settings are determined by the amplitude of the pulse from the bottom MCP. The selected scale factor for each event appears in the telemetry. Finally, the three signals are input to ADCs for conversion to serial digital data for output into the telemetry stream.
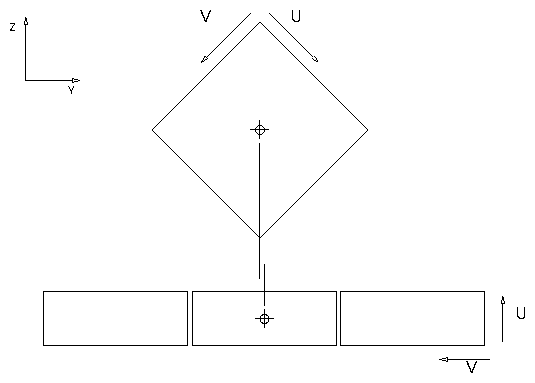
The U axis runs toward the +Y extreme corner while the V axis runs toward the -Y corner.
The HRC-S provides a continuous position readout along the dispersion direction ~ 311 mm long while three MCP segments are required to span this distance. The 1513 wires along the dispersion direction should take ~ 189 taps for complete coverage; the HRC accomplishes this with 64 charge amplifiers by connecting three different taps to a single charge amp and using which MCP segment provided the trigger signal to break the redundancy in coarse position. The U axis uses 16 taps to span its 121 wires. A 100 mm long MCP segment only spans a length of ~ 61 taps and at the gaps between the MCP segments the charge cloud could come from either MCP. Figure 3 shows a schematic layout of the HRC-S position logic[5].
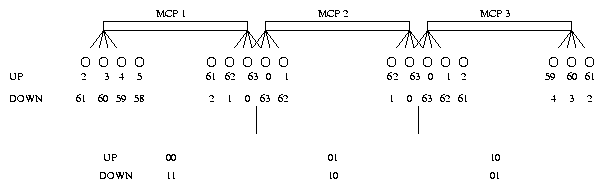
To produce a continuous readout, the logic in table 1 is implemented in the HRC prior to the priority encoding scheme used to determine the coarse position.
| UP Encoding | |||
| MCP | Taps | V-axis Bit 6 | Bit 7 |
| 1 | 2-63 | 0 | 0 |
| 1 | 0-1 | 1 | 0 |
| 2 | 0-63 | 1 | 0 |
| 3 | 62-63 | 1 | 0 |
| 3 | 0-61 | 1 | 1 |
| DOWN Encoding | |||
| MCP | Taps | V-axis Bit 6 | Bit 7 |
| 1 | 0-61 | 1 | 1 |
| 1 | 62-63 | 0 | 1 |
| 2 | 0-63 | 0 | 1 |
| 3 | 0-1 | 0 | 1 |
| 3 | 2-63 | 1 | 0 |
The resulting coarse position range goes from 2 to 189 with the center of the central MCP at a nominal coarse position of 95.5. Events with coarse positions of 64 or 65 could logically come from either MCP 1 or 2, similarly events with coarse positions of 126 or 127 could logically come from either MCP 2 or 3; only the proximity of the edge of the MCP to the tap and the intrinsic resolution of the HRC-S makes one MCP more likely than the other to be the source of the signal. Table 2 lists the nominal ends in coarse position units of the HRC-S MCP segments (based on a nominal central coarse position for MCP 2 of 95.5). Reasonable dividing points for labeling an event as originating on a specific MCP are at coarse positions 64.544 and 126.457.
| Low | High | |
| MCP 1 | 3.224 | 63.965 |
| MCP 2 | 65.122 | 125.878 |
| MCP 3 | 127.035 | 187.792 |
Dr. Michael Juda
Harvard-Smithsonian Center for Astrophysics
60 Garden Street, Mail Stop 70
Cambridge, MA 02138, USA
Ph.: (617) 495-7062
Fax: (617) 495-7356
E-mail: mjuda@cfa.harvard.edu