The heart of the HRC are the microchannel plates (MCP). The process though which incident x-rays are converted to electrical signals is multi-step. Photons which have passed through the UV/Ion Shield will be absorbed by the MCP. The initial photo-electron and Auger electrons produced rapidly lose energy through inelastic scattering and secondary ionization. A fraction of the photons will be absorbed close enough to the surface that at least some of the secondary electrons can escape. If the photon was absorbed in the wall of one of the MCP channels the secondary electrons can escape into the channels, only then can an electrical signal be produced. Once the electrons are in a channel a voltage difference between the front and back surface accelerates them down the channel. The energy gained during acceleration is lost during collisions with the walls of the channel liberating additional charge thereby amplifying the signal. In this memo I will address the yield of secondary electrons per incident photon.
The yield of secondary electrons per photon is determined by a competition between two effects: the depth at which the photon is absorbed and the range of the secondary electrons. If the mean absorption depth is small relative to the electron range we would expect a large yield; conversely a large absorption depth relative to range would result in a small yield. A problem with bare MCPs is that the secondary electron range is small relative to the mean absorption depth. Coating the front MCP with a photocathode that has better range to absorption depth properties is critical to improving the overall detection efficiency of the HRC. Note that it is the inner surface of the channels that must be coated. The HRC-I will use a CsI coating as a photocathode while the HRC-S will use KBr.
Henke, Smith, and Attwood[1] developed a model for the x-ray induced secondary electron emission from photocathodes. Further work by Henke and collaborators[2,3] extended this model and measured the yield at normal incidence for a variety of photocathodes including CsI. They found that the yield was given by
|
When the HRC is behind the HRMA the photons incident on the surface of the MCP will have a distribution of incidence angles with respect to the walls of the MCP channels. The distribution will be a function of the angles between the incoming photons and the axis of the channel; in the HRC this angle will be determined by the bias angle of the MCP channels, the angle of the incident photon relative to the MCP normal, and the angle between the plane of incidence and the plane containing the MCP normal and the channel axis. During laboratory calibrations the HRC will be illuminated with beams of essentially parallel x-rays. Since the wall of the MCP channel is curved there will be a range of incidence angles but this range will be small. The response of the MCP as a function of incident angle will be measured by tilting the HRC with respect to the incoming beam. If the grazing angle of the incoming photons becomes too small reflection of the photons will result in absorption farther down in the channel. As long as this portion of the channel still has a photocathode coating the secondary electron yield should be changed only by the difference in the incidence angle. However the size of the electron cascade may be affected by having less channel length available for charge multiplication.
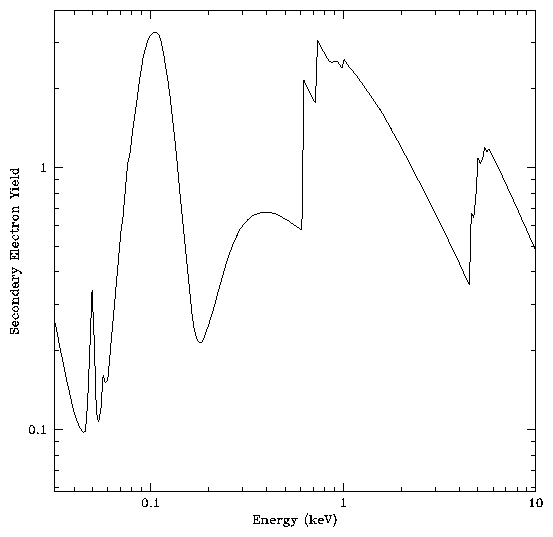
The secondary electron yield of CsI can be modeled using the relation given above, the tabulated atomic constants[4], the measured secondary electron range of 250 Å[3], and scaling to measured values[3]. Figure 1 shows the modeled secondary electron yield for x-rays at normal incidence on a CsI photocathode.

The yield has a rather complicated shape as a function of energy as would be expected from the mass absorption cross section of CsI.
In the HRC the bias angle of the channels in the MCP is nominally 6 degrees. Simply accounting for this angle by assuming that the x-rays are normally incident on the face of the MCP leads to an increase in the yield shown in figure 1 by a factor of ten.
The secondary electron yield of KBr photocathodes has not been measured as well as that of CsI. We can obtain a reasonable first approximation to the yield by using the same secondary electron range and scaling as for CsI. Figure 2 shows the modeled secondary electron yield for x-rays at normal incidence on a KBr photocathode under these assumptions.
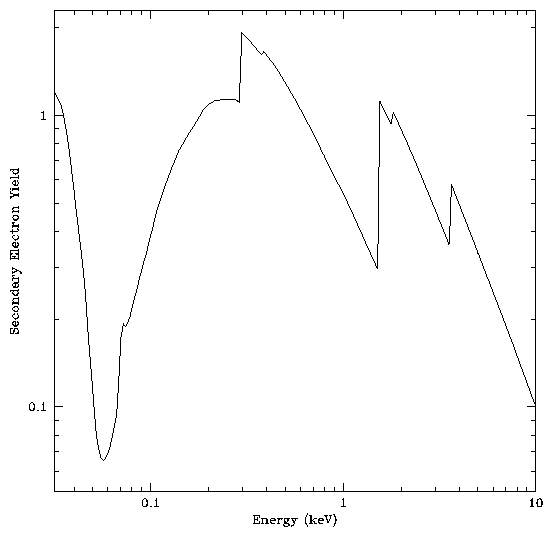
Only the overall scale not the shape of the yield curve as a function of energy is affected by the assumptions made.
There is a considerable amount of structure in the secondary electron yield curves for both photocathodes. Additional structure will be present in the reflectivity curves as a function of angle of the channel walls. These variations should be reflected in the MCP quantum efficiency curves. Measurement of the of the quantum efficiency in the neighborhood of the absorption edges is best accomplished using a monochrometer on a bright continuum source such as a synchrotron. The HRC IPI team is exploring the possibility of testing some ``flight type'' plates at a synchrotron.
The yield vs. photon energy curve has some rather important implications beyond its relevance to the detection efficiency. Since the energy distribution of the secondary electrons is independent of photon energy, the yield contains much of the information on the energy of the incident photon available to the MCP. Unfortunately the yield is not a single valued function of the energy; the same yield is expected at widely seperated energies. HRC pulse height information might not be expected to provide reliable ``two color'' photometry as obtained with the HRI on ROSAT.
Dr. Michael Juda
Harvard-Smithsonian Center for Astrophysics
60 Garden Street, Mail Stop 70
Cambridge, MA 02138, USA
Ph.: (617) 495-7062
Fax: (617) 495-7356
E-mail: mjuda@cfa.harvard.edu