EPHIN Integral Channel PHAs

One possible way of detecting degradation of individual detectors is to look for trends in the PHA distribution from minimum ionizing particles. In the EPHIN we can use the Integral (INT) channel coincidences, those particles that penetrate the entire detector stack (generate signals in detectors A through F) but don't generate a signal in the guard detector (detector G). The INT channel particles are electrons with energies greater than 8.7 MeV, proton with energies greater than 53 MeV, and heavier nuclei with greater than 53 MeV/nucleon. In the figures below EPHIN INT Channel data was selected for times during each orbit when Chandra was at a geocentric distance greater than 80,000 km in order to avoid possible spectral changes associated with radiation belt passages.

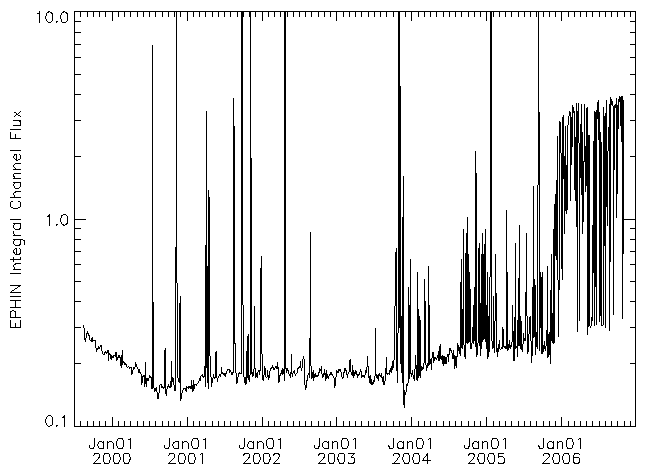
The modulation of the flux due to the solar-activity cycle is evident. This modulation also appears in the median PHAs and dominates any trend that may be due to detector degradation with the possible exception of detector A.

EPHIN Integral Channel Flux
Figure 1: Median EPHIN INT Channel flux

EPHIN Integral Channel Coincidences Detector A Median PHA
Figure 2: Median Detector A PHA for INT Channel Coincidences

EPHIN Integral Channel Coincidences Detector B Median PHA
Figure 3: Median Detector B PHA for INT Channel Coincidences

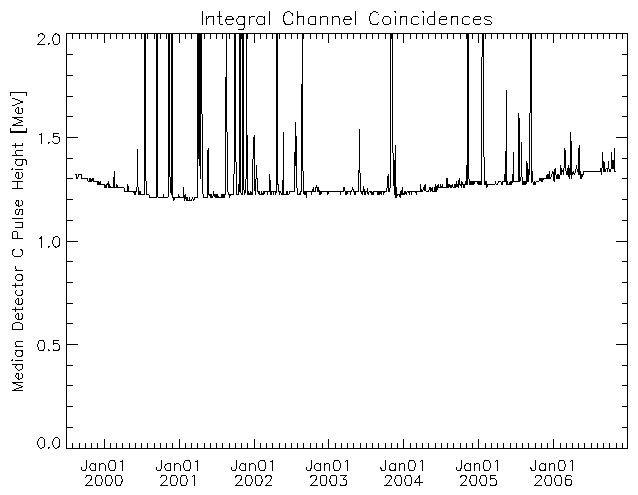
EPHIN Integral Channel Coincidences Detector C Median PHA
Figure 4: Median Detector C PHA for INT Channel Coincidences

EPHIN Integral Channel Coincidences Detector D Median PHA
Figure 5: Median Detector D PHA for INT Channel Coincidences

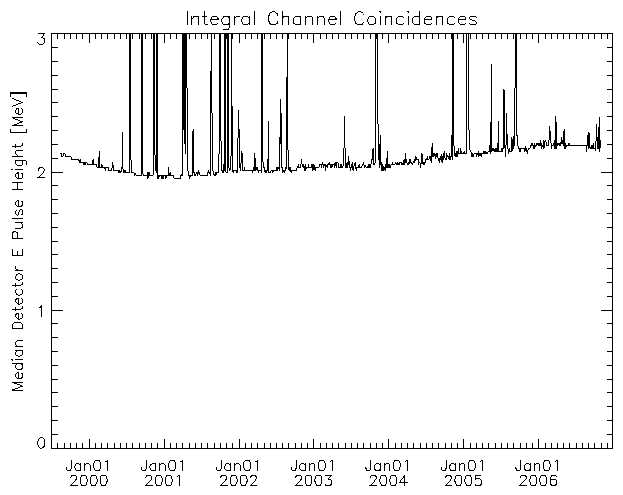
EPHIN Integral Channel Coincidences Detector E Median PHA
Figure 6: Median Detector E PHA for INT Channel Coincidences

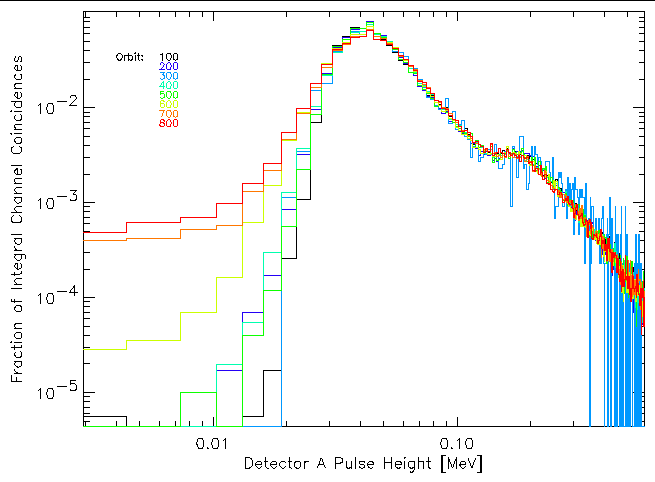
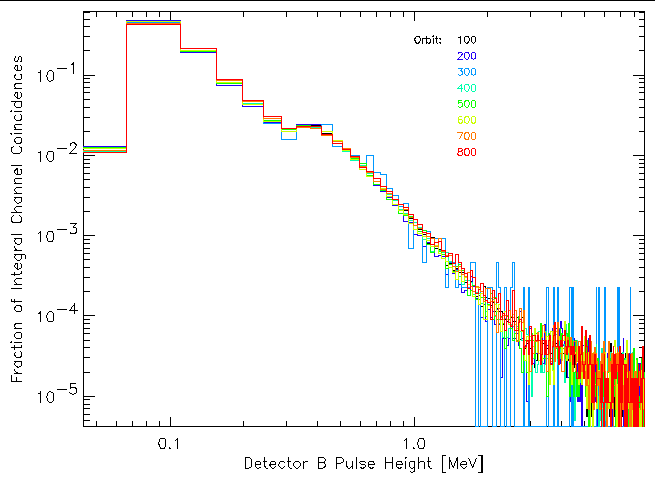
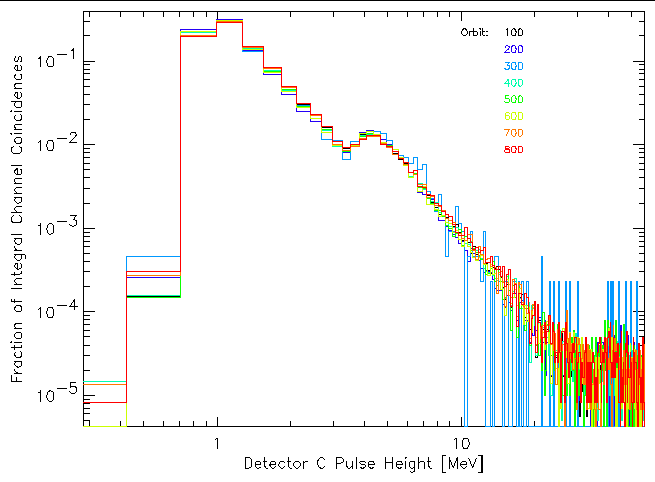
The median pulse height is a simple, easy-to-generate metric but it doesn't tell the whole story. There is more information in the pulse-height distribution that may provide earlier visibility into changes in the detector performance. The plots below the trend (or lack thereof) in the shape of the pulse-height distribution for each of the detectors by plotting the distribution of the Integral channel coincidences for the times when the geocentric distance was greater than 80,000 km for orbits 100, 200, 300, 400, 500, 600, 700, and 800. Only detectors A and E show any significant change in the shape of the pulse-height distributions.

Detector A PHA distributions of Integral channel coincidences
Figure 7: Trend in detector A pulse-height distributions with time (i.e. orbit number). Only Integral channel coincidences are included in the distributions.

Detector B PHA distributions of Integral channel coincidences
Figure 7: Trend in detector B pulse-height distributions with time (i.e. orbit number). Only Integral channel coincidences are included in the distributions.

Detector C PHA distributions of Integral channel coincidences
Figure 7: Trend in detector C pulse-height distributions with time (i.e. orbit number). Only Integral channel coincidences are included in the distributions.

Detector D PHA distributions of Integral channel coincidences
Figure 7: Trend in detector D pulse-height distributions with time (i.e. orbit number). Only Integral channel coincidences are included in the distributions.

Detector E PHA distributions of Integral channel coincidences
Figure 7: Trend in detector E pulse-height distributions with time (i.e. orbit number). Only Integral channel coincidences are included in the distributions.

Last modified: Mon May 1 11:10:56 EDT 2006

Dr. Michael Juda
Harvard-Smithsonian Center for Astrophysics
60 Garden Street, Mail Stop 70
Cambridge, MA 02138, USA
Ph.: (617) 495-7062
Fax: (617) 495-7356
E-mail: mjuda@cfa.harvard.edu