(postsctipt - 4.2MB)
/*AMP_SF Test and Fix */
sum_amps = 0.5*( evt->au1 + evt->au2 + evt->au3 + evt->av1 +
evt->av2 + evt->av3 )/sfparm->amp_gain;
if( evt->pha < 255 ) {
diff1 = fabs(evt->pha - sum_amps);
diff2 = fabs(evt->pha - 2.0*sum_amps);
diff3 = fabs(evt->pha - 4.0*sum_amps);
if( (diff1 <= diff2) && (diff1 <= diff3) &&
(diff1 < sfparm->pha_tol1) ) {
sf = 1;
} else if( (diff2 <= diff1) && (diff2 <= diff3) &&
(diff2 < sfparm->pha_tol2) ) {
sf = 2;
} else if( (diff3 <= diff1) && (diff3 <= diff2) &&
(diff3 < sfparm->pha_tol3) ) {
sf = 3;
} else {
sf = 0;
}
if( sf == 0 ) {
sfparm->ampsf_cnt++;
return(BAD);
}
} else {
sf = 3;
}
if ( sf != evt->amp_sf ) {
sfparm->fixampsf_cnt++;
evt->amp_sf = sf;
}
.
.
.
The key parameters are the gains used to convert summed amplifiers to PHA
(74.0 for HRC-I and 52.9 for HRC-S), and the tolerances for agreement (20 for
HRC-I and 50 for HRC-S - this is a poor guess).
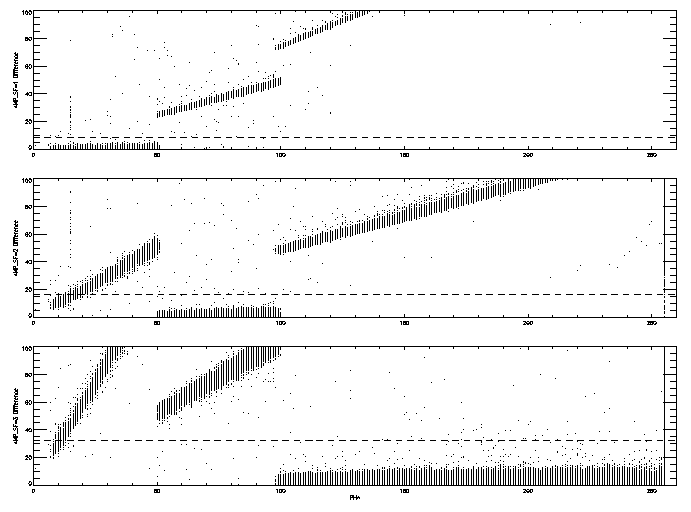
The absolute value of the difference of the scaled sum of the six taps (normalized in gain relative to the PHA scale) is plotted versus PHA for each of the possible scale factors. The horizontal dashed lines are the tolerance band. In this case I used a different "tolerance" on each of the scale ranges (8, 16, and 32 for AMP_SF values of 1, 2, and 3 respectively) rather than the fixed value of 20. This approach can be compared to figure 1 from my earlier memo, where a line forms a boundary between regions of different AMP_SF.
Applying this method to data from the HRC-S is somewhat trickier as the figure below demonstrates. This figure is similar to the one above except that the normalization on the sum of the six taps is different (105.8 instead of 148.0) and the tolerance is 50 for AMP_SF=1 and 2 and 100 for AMP_SF=3.
The potential for mis-identification of the scale factor by this method can be seen in the events with PHA values less than 50. Around these PHA value we expect the events to have AMP_SF values of 1; however, many of the events have difference values near zero when AMP_SF=2. A similar problem exists in the algorithm that I presented in the earlier memo, where a constant slope can clip the lower end of the range of the sum of the tap values at a given PHA (see figure 2 from my earlier memo).
| Total number of events | 135074 |
| Corrected by Method 1 | 324 |
| Corrected by Method 2 | 437 |
| Corrected by Method 1 but not by Method 2 | 5 |
| Corrected by Method 2 but not by Method 1 | 118 |
| Corrected by Method 1 and by Method 2 but different values | 1 |
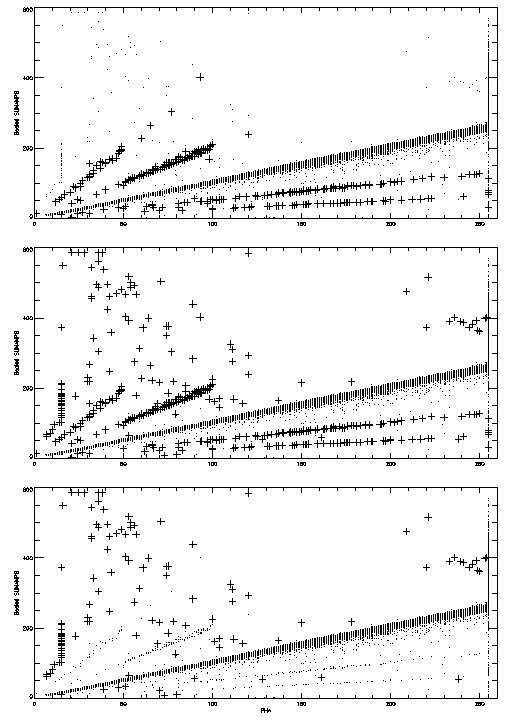
A graphical comparison is shown in the following figure, plotting the
"scaled" sum of the six tap readouts
(SUMAMPS×2AMP_SF-1/148) versus the event PHA. In
all three panes the telemetered values for the amplifier scale are
used rather than the corrected ones. Events that receive a
correction are shown as "+" symbols. In the top pane the "+"
indicates which events were corrected via Method 1; in the middle
pane the "+" indicates those events corrected by Method 2; and in
the bottom pane the "+" indicates events where the two correction
methods yield different results (the 124 events in the last three
row of the table above).
(postscript - 5.9MB)
For the most part the two methods apply corrections to the branches at 1/4×, 1/2×, 2×, and 4× the expected scale factor. As expected, the events that Method 1 does not correct lie outside bands centered on these branches.
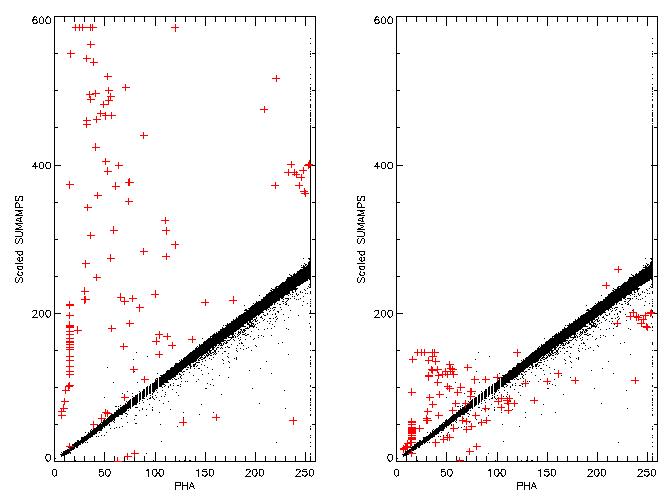
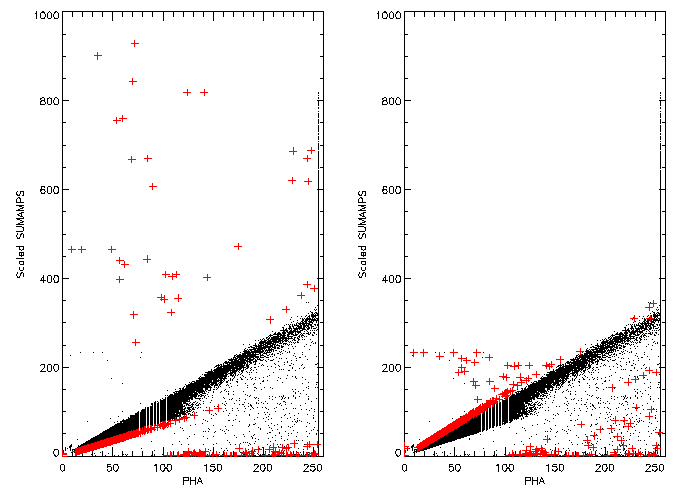
An additional comparison can be made by plotting the scaled sum of the
six taps using the corrected scale factor versus PHA; this is done
in the figure below. The pane on the left was corrected using
Method 1 while the pane on the right used Method 2. In both panes
the red "+" signs indicate the events for which the two methods
yielded different results.
(postscript - 3.8MB)
For the HRC-I both methods perform equally well in correcting the AMP_SF values.
| Total number of events | 130416 |
| Corrected by Method 1 | 6927 |
| Corrected by Method 2 | 8265 |
| Corrected by Method 1 but not by Method 2 | 14 |
| Corrected by Method 2 but not by Method 1 | 1352 |
| Corrected by Method 1 and by Method 2 but different values | 6 |
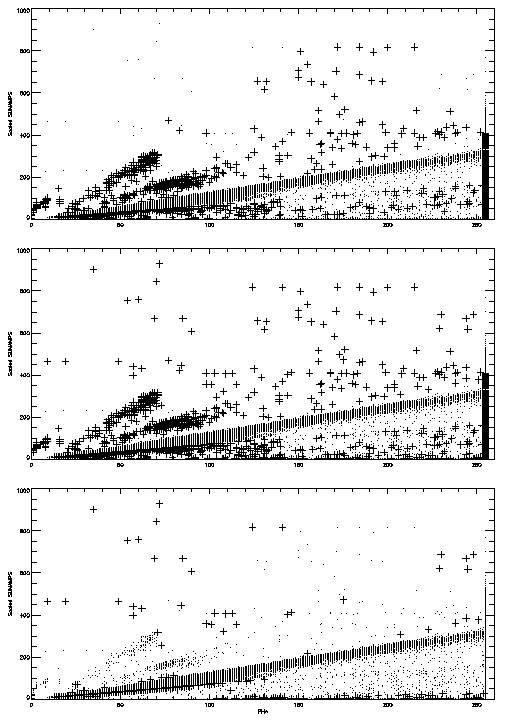
Plots similar to those for the HRC-I comparison are displayed
below. First we plot the scaled sum of the six taps, using the
uncorrected AMP_SF values as a function of PHA. The three panes
once again identify events corrected by Method 1 (top), those
corrected by Method 2 (center), and those where the two methods
gave different results (bottom).
(postscript - 6.2MB)
Below are plots of the scaled sum of the six taps versus PHA after
AMP_SF correction (Method 1 - left, Method 2 - right). The red "+"
symbols identify events where the two method produce different results.
(postscript - 3.8MB)
Once again the results of the two methods are comparable. However, both methods change the AMP_SF value to 2 for many events in the PHA region where we would normally expect a value of 1; Method 2, using a SUMAMPS to PHA ratio of 38, seems to do this for a few more events than Method 1. This mis-assignment is caused by the broad distribution of SUMAMPS at a fixed PHA for low PHA values and is intrinsic to both methods.
Mike Juda Last modified: Wed Aug 8 14:45:16 EDT 2001