


|

|
We have developed a new RMF for the HRC-I and HRC-S using scaled SUMAMPS (SAMP), rather than PHA, as a gain metric. Starting with CALDB 4.2/CIAO 4.2 (December 2009), PI will be calculated from SAMP instead of PHA. For more information about the gain maps used to convert SAMP to PI, see SUMAMPS-based Gain Maps for the HRC-I (Posson-Brown & Kashyap 2009) and A New Gain Map and Pulse-Height Filter for the Chandra LETG/HRC-S Spectrometer (Wargelin 2009).
This page discusses the creation of and justification for the RMF and provides grids in hardness-ratio space for some common spectral models, as calculated with the new RMF.
Vinay Kashyap & Jennifer Posson-Brown
The spectral resolution of the HRC-I is poor compared to the ACIS
detectors, but it does exhibit a non-linear response to photon
energies that can be advantageous in characterizing spectral
hardness. To facilitate this, we have constructed a Redistribution
Matrix file (RMF) that can be used in either Sherpa or XSPEC.
A previous version of the RMF was constructed for use with 256-channel
PI that was derived using PHA. Information about that RMF can be
found here. The new
version is for use with SAMP-derived 1024-channel PI values. For
more information about the gain maps used to convert SAMP to PI,
see Posson-Brown & Kashyap (2009).
HRC-I
Introduction
| Data and Analysis | Files | Grids
December 2009 Introduction
Data and Analysis
Early in the mission, a number of HRC-I/LETG observations were carried
out, giving us an opportunity to directly measure the spectral
response for various photon energies. We use data from observations of
both line and continuum sources (see Table 1).
| Source | ObsIDs | Wavelength Region Used |
| Cyg X-2 | 87 | 1 - 12 AA |
| PKS 2155-304 | 1801, 3716 | 1 - 20 AA |
| HR 1099 | 1388, 1389, 1392, 1393 | 11.5 - 12.5 AA, 17 - 50 AA |
First, we reprocess the data with hrc_process_events to apply the most recent calibration products. Next, we run CIAO tools (v4.1) tgdetect,tg_create_mask and tg_resolve_events on the event lists to assign a wavelength to each event based on its location. Finally, we use the SAMP-based gain maps to calculate PI for each event.
After filtering the data on the wavelength regions listed in Table 1, we combine the background-subtracted datasets, forming a two-dimensional PI/wavelength array. Figure 1 shows the combined spectrum (i.e. the two-dimensional array collapsed onto the wavelength axis). The array is then de-noised by carrying out polynomial fits over a moving window (Loess-type smoothing) along first the PI axis for a slice of wavelengths (over a wavelength range large enough to include 4000 counts in each slice), and then along the wavelength axis for each PI. Figure 2 shows an example of the data along a constant wavelength slice (~7.5 Angstroms) with the polynomial smoothing overplotted in red. Figure 3 shows the residuals between the data array and the smoothed array. The residuals are about +/- 20 counts at most, following with the general shape of the PI spectra, and there aren't any obvious features.



In Figures 4-7 we provide grids in hardness-ratio space for some common spectral models, as calculated using the HRC-I RMF derived above and a nominal on-axis ARF. The grids were calculated using Sherpa. For the hardness ratio, we choose three bands in PI,
Figure 4: Color-color grid for powerlaw model
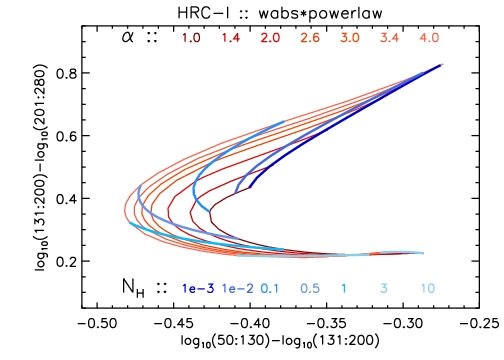
The color-color grid for a powerlaw model, calculated for
various values of the
powerlaw index Gamma (red loci) and
absorption column NH [1022 cm-2] (blue loci).
Figure 5: Color-color grid for low temperature APEC model
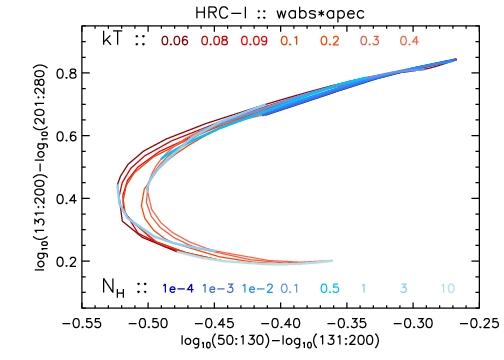
The color-color grid for an APEC model, calculated for
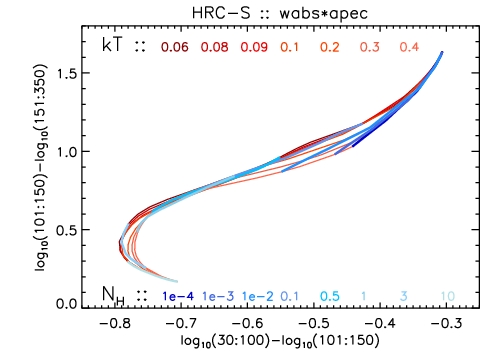
relatively low values of the plasma temperature kT [keV] (red loci) and
absorption column NH [1022 cm-2] (blue loci).
Figure 6: Color-color grid for high temperature APEC model
The color-color grid for an APEC model, calculated for
relatively high values of the plasma temperature kT [keV] (red loci) and
absorption column NH [1022 cm-2] (blue loci).
Figure 7: Color-color grid for blackbody model
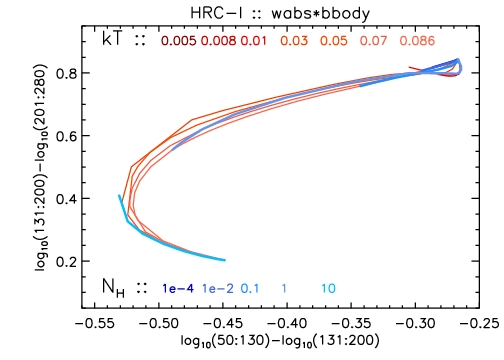
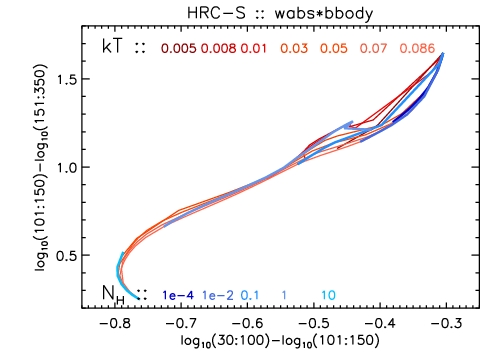
The color-color grid for a Blackbody model, calculated for
various values of the
temperature kT [keV] (red loci) and
absorption column NH [1022 cm-2] (blue loci).
Vinay Kashyap & Jennifer Posson-Brown
October 2010
The spectral resolution of the HRC-S in imaging mode is poor compared to that of the ACIS detectors, but the HRC-S does exhibit a non-linear response to photon energies that can be advantageous in characterizing spectral hardness. To facilitate this, we have constructed a Redistribution Matrix file (RMF) that can be used in either Sherpa or XSPEC. A previous version of the RMF was constructed for use with 256-channel PI that was derived using PHA. Information about that RMF can be found here. The new version is for use with SAMP-derived 1024-channel PI values. For more information about the gain map used to convert SAMP to PI, see HRC-S Gain Map and LETG Background Filter.
| Source | ObsID | PI | Date | Exposure | Wavelength Region Used |
| Capella | 1284 | Calibration | 1999-11-09 | 85.23 ks | 6 - 25 Ang |
| PKS 2155-304 | 331 | Brinkman | 1999-12-25 | 63.16 ks | 10 - 44 Ang |
| RXJ1856.5-3754 | 3380 | Tananbaum | 2001-10-10 | 167.45 ks | 35 - 60 Ang |
| 3381 | 2001-10-12 | 171.07 ks | |||
| 3382 | 2001-10-08 | 101.93 ks | |||
| V4743 Sgr | 3775 | Starrfield | 2003-03-19 | 25.07 ks | 25 - 35 Ang |
| Mkn 421 | 4149 | Nicastro | 2003-07-01 | 99.98 ks | 1 - 15 Ang |
First, we reprocess the data with hrc_process_events (CIAO v4.2, CALDB v4.2) to apply the most recent calibration products, including the time-dependent gain correction which converts scaled-SUMAMPS to PI. We then run tgdetect,tg_create_mask and tg_resolve_events on the event lists to assign a wavelength to each event based on its location.
After filtering the data on the wavelength regions listed in Table 1, we bin the data in wavelength to have approximately 4000 counts per bin after background subtraction. The resulting bin sizes range from ~0.02 to ~1.2 Angstroms, see Figure 1. We then form two-dimensional PI/wavelength arrays for source and background using these wavelength bins and 1 channel PI bins.
Next, the source and background arrays are Loess-smoothed, first along
PI for each wavelength bin then along wavelength for each PI bin. An
example of this smoothing is shown in Figure
2. We then subtracted the smoothed background array (multiplied by
extraction area ratio) from the smoothed source array. Finally, we normalize this net array so that the sum over each wavelength bin is 1. The resulting RMF is shown in Figure 3.



Files
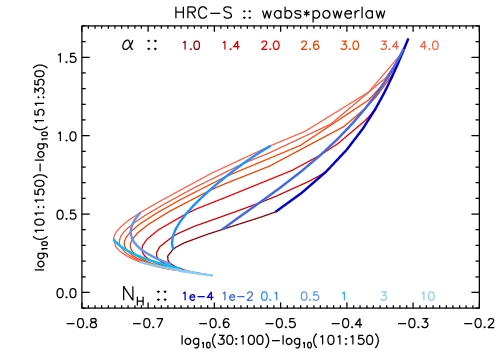
Here we provide hardness-ratio grids for some common spectral models, calculated using the HRC-S RMF derived above and a nominal on-axis ARF. The grids were calculated using Sherpa. For the hardness ratio, we choose three bands in PI,

Last modified: 11/18/13
 |
The Chandra X-Ray
Center (CXC) is operated for NASA by the Smithsonian Astrophysical Observatory. 60 Garden Street, Cambridge, MA 02138 USA. Email: cxcweb@head.cfa.harvard.edu Smithsonian Institution, Copyright © 1998-2004. All rights reserved. |